Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-27T18:42:00.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Unifying constitutive law of vibroconvective turbulence in microgravity

Published online by Cambridge University Press:  16 May 2024

Ze-Lin Huang ,
Jian-Zhao Wu Open the ORCID record for Jian-Zhao Wu [Opens in a new window] ,
Xi-Li Guo ,
Chao-Ben Zhao ,
Bo-Fu Wang Open the ORCID record for Bo-Fu Wang [Opens in a new window] ,
Kai Leong Chong Open the ORCID record for Kai Leong Chong [Opens in a new window]  and
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]
Ze-Lin Huang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Jian-Zhao Wu*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China Shanghai Institute of Aircraft Mechanics and Control, Zhangwu Road, Shanghai 200092, PR China
Xi-Li Guo
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Chao-Ben Zhao
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Bo-Fu Wang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Kai Leong Chong
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China Shanghai Institute of Aircraft Mechanics and Control, Zhangwu Road, Shanghai 200092, PR China
Quan Zhou*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

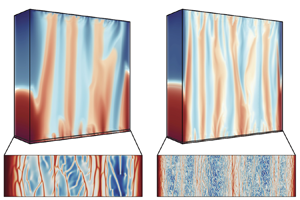
We report the unified constitutive law of vibroconvective turbulence in microgravity, i.e. $Nu \sim a^{-1} Re_{os}^\beta$ where the Nusselt number $Nu$ measures the global heat transport, $a$ is the dimensionless vibration amplitude, $Re_{os}$ is the oscillational Reynolds number and $\beta$ is the universal exponent. We find that the dynamics of boundary layers plays an essential role in vibroconvective heat transport and the $Nu$-scaling exponent $\beta$ is determined by the competition between the thermal boundary layer (TBL) and vibration-induced oscillating boundary layer (OBL). Then a physical model is proposed to explain the change of scaling exponent from $\beta =2$ in the TBL-dominant regime to $\beta = 4/3$ in the OBL-dominant regime. Our finding elucidates the emergence of universal constitutive laws in vibroconvective turbulence, and opens up a new avenue for generating a controllable effective heat transport under microgravity or even microfluidic environment in which the gravity effect is nearly absent.

JFM classification

Convection: Convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 987 , 25 May 2024 , A14
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., et al. 2022 Aspect ratio dependence of heat transfer in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 128 (8), 084501.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Amiroudine, S. & Beysens, D. 2008 Thermovibrational instability in supercritical fluids under weightlessness. Phys. Rev. E 78 (3), 036325.CrossRefGoogle ScholarPubMed
Apffel, B., Hidalgo-Caballero, S., Eddi, A. & Fort, E. 2021 Liquid walls and interfaces in arbitrary directions stabilized by vibrations. Proc. Natl Acad. Sci. USA 118 (48), e2111214118.CrossRefGoogle ScholarPubMed
Apffel, B., Novkoski, F., Eddi, A. & Fort, E. 2020 Floating under a levitating liquid. Nature 585 (7823), 48–52.CrossRefGoogle Scholar
Beysens, D. 2006 Vibrations in space as an artificial gravity? Europhys. News 37 (3), 22–25.CrossRefGoogle Scholar
Beysens, D., Chatain, D., Evesque, P. & Garrabos, Y. 2005 High-frequency driven capillary flows speed up the gas–liquid phase transition in zero-gravity conditions. Phys. Rev. Lett. 95 (3), 034502.CrossRefGoogle ScholarPubMed
Blass, A., Zhu, X., Verzicco, R., Lohse, D. & Stevens, R.J. 2020 Flow organization and heat transfer in turbulent wall sheared thermal convection. J. Fluid Mech. 897, A22.CrossRefGoogle ScholarPubMed
Brunet, P., Eggers, J. & Deegan, R.D. 2007 Vibration-induced climbing of drops. Phys. Rev. Lett. 99, 144501.CrossRefGoogle ScholarPubMed
Chen, X., Wang, D.-P. & Xi, H.-D. 2020 Reduced flow reversals in turbulent convection in the absence of corner vortices. J. Fluid Mech. 891, R5.CrossRefGoogle Scholar
Chong, K.L., Qiao, S., Wu, J.-Z. & Wang, B.-F. 2024 Heat transfer enhancement in vertical convection under spatially harmonic temperature modulation. Intl J. Heat Mass Transfer 227, 125452.CrossRefGoogle Scholar
Cissé, I., Bardan, G. & Mojtabi, A. 2004 Rayleigh–Bénard convective instability of a fluid under high-frequency vibration. Intl J. Heat Mass Transfer 47 (19–20), 4101–4112.CrossRefGoogle Scholar
Crewdson, G. & Lappa, M. 2021 Thermally-driven flows and turbulence in vibrated liquids. Intl J. Thermofluids 11, 100102.CrossRefGoogle Scholar
Daniel, S., Chaudhury, M.K. & De Gennes, P.-G. 2005 Vibration-actuated drop motion on surfaces for batch microfluidic processes. Langmuir 21 (9), 4240–4248.CrossRefGoogle ScholarPubMed
Ecke, R.E. & Shishkina, O. 2023 Turbulent rotating Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 55, 603–638.CrossRefGoogle Scholar
Gaponenko, Y., Torregrosa, M., Yasnou, V., Mialdun, A. & Shevtsova, V. 2015 Interfacial pattern selection in miscible liquids under vibration. Soft Matt. 11 (42), 8221–8224.CrossRefGoogle ScholarPubMed
Garrabos, Y., Beysens, D., Lecoutre, C., Dejoan, A., Polezhaev, V. & Emelianov, V. 2007 Thermoconvectional phenomena induced by vibrations in supercritical SF$_6$ under weightlessness. Phys. Rev. E 75 (5), 056317.CrossRefGoogle Scholar
Gershuni, G.Z. & Lyubimov, D.V. 1998 Thermal Vibrational Convection. Wiley & Sons.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
Guo, X.-L., Wu, J.-Z., Wang, B.-F., Zhou, Q. & Chong, K.L. 2023 Flow structure transition in thermal vibrational convection. J. Fluid Mech. 974, A29.CrossRefGoogle Scholar
Guo, X.-Q., Wang, B.-F., Wu, J.-Z., Chong, K.L. & Zhou, Q. 2022 Turbulent vertical convection under vertical vibration. Phys. Fluids 34, 055106.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108 (2), 024502.CrossRefGoogle Scholar
Hirata, K., Sasaki, T. & Tanigawa, H. 2001 Vibrational effects on convection in a square cavity at zero gravity. J. Fluid Mech. 445, 327–344.CrossRefGoogle Scholar
Huang, Y.-X. & Zhou, Q. 2013 Counter-gradient heat transport in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 737, R3.CrossRefGoogle Scholar
Huang, Z.-L., Guo, X.-L., Wu, J.-Z., Wang, B.-F., Chong, K.L. & Zhou, Q. 2023 Rayleigh-number dependence of the critical vibration frequency in vibrating thermal turbulence. Phys. Rev. Fluids 8 (11), 113501.CrossRefGoogle Scholar
Iyer, K.P., Scheel, J.D., Schumacher, J. & Sreenivasan, K.R. 2020 Classical $1/3$ scaling of convection holds up to $Ra=10^{15}$. Proc. Natl Acad. Sci. USA 117 (14), 7594–7598.CrossRefGoogle ScholarPubMed
Jiang, H., Wang, D., Liu, S. & Sun, C. 2022 Experimental evidence for the existence of the ultimate regime in rapidly rotating turbulent thermal convection. Phys. Rev. Lett. 129 (20), 204502.CrossRefGoogle ScholarPubMed
Jiang, H., Zhu, X., Wang, D., Huisman, S.G. & Sun, C. 2020 Supergravitational turbulent thermal convection. Sci. Adv. 6 (40), eabb8676.CrossRefGoogle ScholarPubMed
Jin, T.-C., Wu, J.-Z., Zhang, Y.-Z., Liu, Y.-L. & Zhou, Q. 2022 Shear-induced modulation on thermal convection over rough plates. J. Fluid Mech. 936, A28.CrossRefGoogle Scholar
Lepot, S., Aumaître, S. & Gallet, B. 2018 Radiative heating achieves the ultimate regime of thermal convection. Proc. Natl Acad. Sci. USA 115 (36), 8937–8941.CrossRefGoogle ScholarPubMed
Li, Y.-Z., Chen, X. & Xi, H.-D. 2024 Enhanced heat transfer and reduced flow reversals in turbulent thermal convection with an obstructed centre. J. Fluid Mech. 981, A16.CrossRefGoogle Scholar
Li, Y.-Z., Chen, X., Xu, A. & Xi, H.-D. 2022 Counter-flow orbiting of the vortex centre in turbulent thermal convection. J. Fluid Mech. 935, A19.CrossRefGoogle Scholar
Melnikov, D., Ryzhkov, I., Mialdun, A. & Shevtsova, V. 2008 Thermovibrational convection in microgravity: preparation of a parabolic flight experiment. Microgravity Sci. Technol. 20, 29–39.CrossRefGoogle Scholar
Meng, W.-S., Zhao, C.-B., Wu, J.-Z., Wang, B.-F., Zhou, Q. & Chong, K.L. 2024 Simulation of flow and debris migration in extreme ultraviolet source vessel. Phys. Fluids 36 (2), 023322.CrossRefGoogle Scholar
Mialdun, A., Ryzhkov, I., Melnikov, D. & Shevtsova, V. 2008 Experimental evidence of thermal vibrational convection in a nonuniformly heated fluid in a reduced gravity environment. Phys. Rev. Lett. 101 (8), 084501.CrossRefGoogle Scholar
Monti, R., Savino, R. & Lappa, M. 2001 On the convective disturbances induced by g-jitter on the space station. Acta Astronaut. 48 (5–12), 603–615.CrossRefGoogle Scholar
Pesch, W., Palaniappan, D., Tao, J. & Busse, F.H. 2008 Convection in heated fluid layers subjected to time-periodic horizontal accelerations. J. Fluid Mech. 596, 313–332.CrossRefGoogle Scholar
Plumley, M. & Julien, K. 2019 Scaling laws in Rayleigh–Bénard convection. Earth Space Sci. 6 (9), 1580–1592.CrossRefGoogle Scholar
Rogers, J.L., Schatz, M.F., Bougie, J.L. & Swift, J.B. 2000 a Rayleigh–Bénard convection in a vertically oscillated fluid layer. Phys. Rev. Lett. 84 (1), 87.CrossRefGoogle Scholar
Rogers, J.L., Schatz, M.F., Brausch, O. & Pesch, W. 2000 b Superlattice patterns in vertically oscillated Rayleigh–Bénard convection. Phys. Rev. Lett. 85 (20), 4281.CrossRefGoogle ScholarPubMed
Salgado Sánchez, P., Gaponenko, Y.A., Porter, J. & Shevtsova, V. 2019 Finite-size effects on pattern selection in immiscible fluids subjected to horizontal vibrations in weightlessness. Phys. Rev. E 99, 042803.CrossRefGoogle ScholarPubMed
Sánchez, P.S., Gaponenko, Y., Yasnou, V., Mialdun, A., Porter, J. & Shevtsova, V. 2020 Effect of initial interface orientation on patterns produced by vibrational forcing in microgravity. J. Fluid Mech. 884, A38.Google Scholar
Sánchez, P.S., Yasnou, V., Gaponenko, Y., Mialdun, A., Porter, J. & Shevtsova, V. 2019 Interfacial phenomena in immiscible liquids subjected to vibrations in microgravity. J. Fluid Mech. 865, 850–883.CrossRefGoogle Scholar
Savino, R., Monti, R. & Piccirillo, M. 1998 Thermovibrational convection in a fluid cell. Comput. Fluids 27 (8), 923–939.CrossRefGoogle Scholar
Scagliarini, A., Gylfason, Á. & Toschi, F. 2014 Heat-flux scaling in turbulent Rayleigh–Bénard convection with an imposed longitudinal wind. Phys. Rev. E 89 (4), 043012.CrossRefGoogle ScholarPubMed
Sharma, D., Erriguible, A., Gandikota, G., Beysens, D. & Amiroudine, S. 2019 Vibration-induced thermal instabilities in supercritical fluids in the absence of gravity. Phys. Rev. Fluids 4 (3), 033401.CrossRefGoogle Scholar
Shevtsova, V., Ryzhkov, I.I., Melnikov, D.E., Gaponenko, Y.A. & Mialdun, A. 2010 Experimental and theoretical study of vibration-induced thermal convection in low gravity. J. Fluid Mech. 648, 53–82.CrossRefGoogle Scholar
Sreenivasan, K.R. 2019 Turbulent mixing: a perspective. Proc. Natl Acad. Sci. USA 116 (37), 18175–18183.CrossRefGoogle ScholarPubMed
Stevens, R.J., van der Poel, E.P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.CrossRefGoogle Scholar
Swaminathan, A., Garrett, S.L., Poese, M.E. & Smith, R.W. 2018 Dynamic stabilization of the Rayleigh–Bénard instability by acceleration modulation. J. Acoust. Soc. Am. 144 (4), 2334–2343.CrossRefGoogle ScholarPubMed
Toppaladoddi, S., Succi, S. & Wettlaufer, J.S. 2017 Roughness as a route to the ultimate regime of thermal convection. Phys. Rev. Lett. 118 (7), 074503.CrossRefGoogle Scholar
Wang, B.-F., Zhou, Q. & Sun, C. 2020 Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 6 (21), eaaz8239.CrossRefGoogle ScholarPubMed
Wang, Z., Calzavarini, E., Sun, C. & Toschi, F. 2021 How the growth of ice depends on the fluid dynamics underneath. Proc. Natl Acad. Sci. USA 118 (10), e2012870118.CrossRefGoogle ScholarPubMed
Wang, Z., Mathai, V. & Sun, C. 2019 Self-sustained biphasic catalytic particle turbulence. Nat. Commun. 10, 3333.CrossRefGoogle ScholarPubMed
Wu, J.-Z., Dong, Y.-H., Wang, B.-F. & Zhou, Q. 2021 Phase decomposition analysis on oscillatory Rayleigh–Bénard turbulence. Phys. Fluids 33 (4), 045108.CrossRefGoogle Scholar
Wu, J.-Z., Wang, B.-F., Chong, K.L., Dong, Y.-H., Sun, C. & Zhou, Q. 2022 a Vibration-induced ‘anti-gravity’ tames thermal turbulence at high Rayleigh numbers. J. Fluid Mech. 951, A13.CrossRefGoogle Scholar
Wu, J.-Z., Wang, B.-F. & Zhou, Q. 2022 b Massive heat transfer enhancement of Rayleigh–Bénard turbulence over rough surfaces and under horizontal vibration. Acta Mech. Sin. 38, 321319.CrossRefGoogle Scholar
Xi, H.-D., Zhang, Y.-B., Hao, J.-T. & Xia, K.-Q. 2016 Higher-order flow modes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 805, 31–51.CrossRefGoogle Scholar
Xu, A., Xu, B.-R. & Xi, H.-D. 2023 Wall-sheared thermal convection: heat transfer enhancement and turbulence relaminarization. J. Fluid Mech. 960, A2.CrossRefGoogle Scholar
Zhang, Y. & Zhou, Q. 2024 Low-Prandtl-number effects on global and local statistics in two-dimensional Rayleigh–Bénard convection. Phys. Fluids 36, 015107.CrossRefGoogle Scholar
Zhang, Y., Zhou, Q. & Sun, C. 2017 Statistics of kinetic and thermal energy dissipation rates in two-dimensional turbulent Rayleigh–Bénard convection. J. Fluid Mech. 814, 165–184.CrossRefGoogle Scholar
Zhang, Y.-Z., Sun, C., Bao, Y. & Zhou, Q. 2018 How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 836, R2.CrossRefGoogle Scholar
Zhao, C.-B., Wang, B.-F., Wu, J.-Z., Chong, K.L. & Zhou, Q. 2022 Suppression of flow reversals via manipulating corner rolls in plane Rayleigh–Bénard convection. J. Fluid Mech. 946, A44.CrossRefGoogle Scholar
Zhao, C.-B., Wu, J.-Z., Wang, B.-F., Chang, T., Zhou, Q. & Chong, K.L. 2024 Numerical study on the onset of global-scale flow from individual buoyant plumes: implications for indoor disease transmission. Phys. Fluids 36 (3), 035149.CrossRefGoogle Scholar
Zou, S. & Yang, Y. 2021 Realizing the ultimate scaling in convection turbulence by spatially decoupling the thermal and viscous boundary layers. J. Fluid Mech. 919, R3.CrossRefGoogle Scholar
Zyuzgin, A., Ivanov, A., Polezhaev, V., Putin, G. & Soboleva, E. 2001 Convective motions in near-critical fluids under real zero-gravity conditions. Cosmic Res. 39 (2), 175–186.CrossRefGoogle Scholar
Supplementary material: File

Huang et al. supplementary movie 1

Instantaneous flow structures visualized by volume rendering of temperature anomaly in three-dimensional microgravity vibroconvection at ω = 105, a = 10-2 and Pr=4.38, corresponding to figure 1(a) left. The time is scaled by the vibration period.
Download Huang et al. supplementary movie 1(File)
File 7.2 MB
Supplementary material: File

Huang et al. supplementary movie 2

Instantaneous flow structures visualized by volume rendering of temperature anomaly in three-dimensional microgravity vibroconvection at ω = 106, a = 10-2 and Pr=4.38, corresponding to figure 1(a) middle. The time is scaled by the vibration period.
Download Huang et al. supplementary movie 2(File)
File 4 MB
Supplementary material: File

Huang et al. supplementary movie 3

Instantaneous flow structures visualized by volume rendering of temperature anomaly in three-dimensional microgravity vibroconvection at ω = 107, a = 10-2 and Pr=4.38, corresponding to figure 1(a) right. The time is scaled by the vibration period.
Download Huang et al. supplementary movie 3(File)
File 5.3 MB