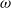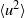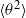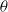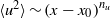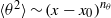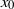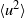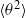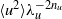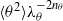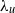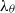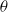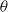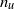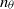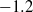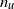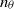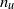We investigate dynamo action for a parallel flow of an electrically conducting fluid located over a boundary with spatially varying magnetic permeability. We first compute the dynamo threshold numerically. Then we perform an asymptotic expansion in the limit of small permeability modulation, which gives accurate results even for moderate modulation. We present in detail the mechanism at work for this dynamo. It is an interplay between shear (an 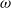$\omega $-effect) and a new conversion mechanism that originates from the non-uniform magnetic boundary. We illustrate how a similar mechanism leads to dynamo action in the case of spatially modulated electrical conductivity, a problem studied by Busse & Wicht (Geophys. Astrophys. Fluid Dyn., vol. 64, 1992, pp. 135–144). Finally, we discuss the relevance of this effect to experimental dynamos and present ways to increase the dynamo efficiency and reduce the instability threshold.

Flow instabilities encountered in the homogeneous cooling of a gas–solid system are considered via lattice-Boltzmann simulations. Unlike previous efforts, the relative contribution of the two mechanisms leading to instabilities is explored: viscous dissipation (fluid-phase effects) and collisional dissipation (particle-phase effects). The results indicate that the instabilities encountered in the gas–solid system mimic those previously observed in their granular (no fluid) counterparts, namely a velocity vortex instability that precedes in time a clustering instability. We further observe that the onset of the instabilities is quicker in more dissipative systems, regardless of the source of the dissipation. Somewhat surprisingly however, a cross-over of the kinetic energy levels is observed during the evolution of the instability. Specifically, the kinetic energy of the gas–solid system is seen to become greater than that of its granular counterpart (i.e. same restitution coefficient) after the vortex instability sets in. This cross-over of kinetic energy levels between a more dissipative system (gas–solid) and a less dissipative system (granular) can be explained by the alignment of particle motion found in a vortex. Such alignment leads to a reduction in both collisional and viscous energy dissipation due to the more glancing nature of collisions.

The paper examines the validity of velocity and scalar invariants in slightly heated and approximately isotropic turbulence generated by passive conventional grids. By assuming that the variances $\langle {u}^{2} \rangle $ and $\langle {\theta }^{2} \rangle $ ($u$ and $\theta $ represent the longitudinal velocity and temperature fluctuations) decay along the streamwise direction $x$ according to power laws $\langle {u}^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{u} } $ and $\langle {\theta }^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{\theta } } $ (${x}_{0} $ is the virtual origin of the flow) and with the further assumption that the one-point energy and scalar variance budgets are represented closely by a balance between the rates of change of $\langle {u}^{2} \rangle $ and $\langle {\theta }^{2} \rangle $ and the corresponding mean energy dissipation rates, the products $\langle {u}^{2} \rangle { \lambda }_{u}^{- 2{n}_{u} } $ and $\langle {\theta }^{2} \rangle { \lambda }_{\theta }^{- 2{n}_{\theta } } $ must remain constant with respect to $x$. Here ${\lambda }_{u} $ and ${\lambda }_{\theta } $ are the Taylor and Corrsin microscales. This is unambiguously supported by previously available data, as well as new measurements of $u$ and $\theta $ made at small Reynolds numbers downstream of three different biplane grids. Implications for invariants based on measured integral length scales of $u$ and $\theta $ are also tested after confirming that the dimensionless energy and scalar variance dissipation rate parameters are approximately constant with $x$. Since the magnitudes of ${n}_{u} $ and ${n}_{\theta } $ vary from grid to grid and may also depend on the Reynolds number, the Saffman and Corrsin invariants which correspond to a value of $- 1. 2$ for ${n}_{u} $ and ${n}_{\theta } $ are unlikely to apply in general. The effect of the Reynolds number on ${n}_{u} $ is discussed in the context of published data for both passive and active grids.

A compact nonlinear expression for the velocity spectra of homogeneous mean shear flow is derived by means of a simplified two-point closure. It applies to all scales and times. The derived equation can be viewed as a nonlinear extension of the linear, rapid-distortion-theory (RDT) equation. The principal simplification is to model the nonlinear pressure–strain rate as first-order in the spectral anisotropy: a spectral Rotta-equation. This simplified equation and its solution are expressed in terms of the RDT solution. That solution helps reveal the role of nonlinearity. An equation for the velocity spectrum is then obtained at all scales and times. A dominant characteristic predicted for nonlinear behaviour is that the turbulence energy grows exponentially with time, with the spectrum simultaneously moving to smaller and smaller wavenumbers. The nonlinear growth rate is determined. Other analytical predictions of the derived equation include: the conditions for self-similarity; local isotropy; various properties of mean shear flow, including characteristic energy, length and temporal growth scales; and a critique of perturbation theory. Comparisons are made with laboratory experiments and direct numerical simulations. Although the theory applies to all scales and times, including an exact expression for RDT, the calculations are focused on nonlinear behaviour at large times. Several approximations used in this work are examined.