Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-02T21:09:20.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants for slightly heated decaying grid turbulence

Published online by Cambridge University Press:  26 June 2013

R. A. Antonia ,
S. K. Lee ,
L. Djenidi ,
P. Lavoie  and
L. Danaila
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW, 2308, Australia
S. K. Lee
Affiliation:
School of Engineering, University of Newcastle, NSW, 2308, Australia
L. Djenidi*
Affiliation:
School of Engineering, University of Newcastle, NSW, 2308, Australia
P. Lavoie
Affiliation:
Institute for Aerospace Studies, University of Toronto, ON, Canada M3H 5T6
L. Danaila
Affiliation:
CORIA CNRS UMR 6614, Université de Rouen, 77801 Saint Etienne du Rouvray, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

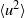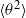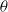The paper examines the validity of velocity and scalar invariants in slightly heated and approximately isotropic turbulence generated by passive conventional grids. By assuming that the variances $\langle {u}^{2} \rangle $ and $\langle {\theta }^{2} \rangle $ ($u$ and $\theta $ represent the longitudinal velocity and temperature fluctuations) decay along the streamwise direction $x$ according to power laws 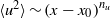$\langle {u}^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{u} } $ and 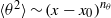$\langle {\theta }^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{\theta } } $ (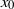${x}_{0} $ is the virtual origin of the flow) and with the further assumption that the one-point energy and scalar variance budgets are represented closely by a balance between the rates of change of 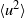$\langle {u}^{2} \rangle $ and 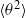$\langle {\theta }^{2} \rangle $ and the corresponding mean energy dissipation rates, the products 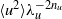$\langle {u}^{2} \rangle { \lambda }_{u}^{- 2{n}_{u} } $ and 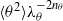$\langle {\theta }^{2} \rangle { \lambda }_{\theta }^{- 2{n}_{\theta } } $ must remain constant with respect to $x$. Here 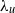${\lambda }_{u} $ and 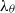${\lambda }_{\theta } $ are the Taylor and Corrsin microscales. 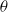This is unambiguously supported by previously available data, as well as new measurements of $u$ and $\theta $ made at small Reynolds numbers downstream of three different biplane grids. 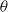Implications for invariants based on measured integral length scales of $u$ and $\theta $ are also tested after confirming that the dimensionless energy and scalar variance dissipation rate parameters are approximately constant with $x$. Since the magnitudes of 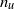${n}_{u} $ and 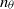${n}_{\theta } $ vary from grid to grid and may also depend on the Reynolds number, the Saffman and Corrsin invariants which correspond to a value of 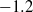$- 1. 2$ for 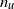${n}_{u} $ and 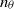${n}_{\theta } $ are unlikely to apply in general. The effect of the Reynolds number on 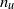${n}_{u} $ is discussed in the context of published data for both passive and active grids.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 727 , 25 July 2013 , pp. 379 - 406
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Browne, L. W. B. & Chambers, A. J. 1981 Determination of time constants of cold wires. Rev. Sci. Instrum. 52 (9), 1382–1385.Google Scholar
Antonia, R. A., Lavoie, P., Djenidi, L. & Benaissa, A. 2010 Effect of a small axisymmetric contraction on grid turbulence. Exp. Fluids 49, 3–10.Google Scholar
Antonia, R. A. & Orlandi, P. 2004 Similarity of decaying isotropic turbulence with a passive scalar. J. Fluid Mech. 505, 123–151.Google Scholar
Antonia, R. A., Ould-Rouis, M., Anselmet, F. & Zhu, Y. 1997 Analogy between predictions of Kolmogorov and Yaglom. J. Fluid Mech. 332, 395–409.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2003 Similarity of energy structure functions in decaying homogeneous isotropic turbulence. J. Fluid Mech. 487, 245–269.Google Scholar
Antonia, R. A., Smalley, R. J., Zhou, T., Anselmet, F. & Danaila, L. 2004 Similarity solution of temperature structure functions in decaying homogeneous isotropic turbulence. Phys. Rev. E 69, 016305.CrossRefGoogle ScholarPubMed
Antonia, R. A., Zhou, T., Danaila, L. & Anselmet, F. 2000 Streamwise inhomogeneity of decaying grid turbulence. Phys. Fluids 12 (11), 3086–3089.Google Scholar
Antonia, R. A., Zhou, T. & Zhu, Y. 1998 Three-component vorticity measurements in a turbulent grid flow. J. Fluid Mech. 374, 29–57.Google Scholar
Antonia, R. A., Zhu, Y., Anselmet, F. & Ould-Rouis, M. 1996 Comparison between the sum of second-order velocity structure functions and the second-order temperature structure function. Phys. Fluids 8 (11), 3105–3111.Google Scholar
Batchelor, G. K. 1948 Energy decay and self-preserving correlation functions in isotropic turbulence. Quart. Appl. Maths. 6, 97–116.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Proudman, I. 1956 The large-scale structure of homogeneous turbulence. Philos. Trans. R. Soc. Lond. Ser. A 248 (949), 369–405.Google Scholar
Bennett, J. C. & Corrsin, S. 1978 Small Reynolds number nearly isotropic turbulence in a straight duct and a contraction. Phys. Fluids 21 (12), 2129–2140.Google Scholar
Birkhoff, G. 1954 Fourier Synthesis of Homogeneous Turbulence. Commun. Pure Appl. Maths. 7, 19–44.Google Scholar
Browne, L. W. B. & Antonia, R. A. 1987 The effect of wire length on temperature statistics in a turbulent wake. Exp. Fluids 5, 426–428.Google Scholar
Burattini, P., Lavoie, P., Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 Power law of decaying homogeneous isotropic turbulence at low Reynolds number. Phys. Rev. E 73, 066304.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.CrossRefGoogle Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25 (4), 657–682.Google Scholar
Corrsin, S. 1951 The decay of isotropic temperature fluctuations in an isotropic turbulence. J. Aeronaut. Sci. 18 (6), 417–423.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Danaila, L., Antonia, R. A. & Burattini, P. 2004 Progress in studying small-scale turbulence using ‘exact’ two-point equations. New J. Phys. 6 (128).Google Scholar
Danaila, L., Zhou, T., Anselmet, F. & Antonia, R. A. 2000 Calibration of a temperature dissipation probe in decaying grid turbulence. Exp. Fluids 28, 45–50.CrossRefGoogle Scholar
Davidson, P. A. 2000 Was Loitsyansky correct? A review of the arguments. J. Turbul. 1 (6), 1–14.Google Scholar
Davidson, P. A. 2009 The role of angular momentum conservation in homogeneous turbulence. J. Fluid Mech. 632, 329–358.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Fulachier, L. & Antonia, R. A. 1984 Spectral analogy between temperature and velocity fluctuations in several turbulent flows. Intl J. Heat Mass Transfer 27 (7), 987–997.Google Scholar
George, W. K. 1992a Self-preservation of temperature fluctuations in isotropic turbulence. In Studies in Turbulence, pp. 514–528. Springer.Google Scholar
George, W. K. 1992b The decay of homogeneous isotropic turbulence. Phys. Fluids 4 (7), 1492–1509.Google Scholar
George, W. K. & Davidson, L. 2004 Role of initial conditions in establishing asymptotic flow behaviour. AIAA J. 42 (3), 438–446.Google Scholar
Gonzalez, G. & Fall, A. 1998 The approach to self-preservation of scalar fluctuations decay in isotropic turbulence. Phys. Fluids 10, 654–661.Google Scholar
Hinze, J. O. 1975 Turbulence. McGraw-Hill.Google Scholar
Huang, M.-J. & Leonard, A. 1994 Power-law decay of homogeneous turbulence at low Reynolds number. Phys. Fluids 6 (11), 3765–3775.Google Scholar
Ishida, T., Davidson, P. A. & Kaneda, Y. 2006 On the decay of isotropic turbulence. J. Fluid Mech. 564, 455–475.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Kármán, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 164 (917), 192–215.Google Scholar
Kistler, A. L. & Vrebalovich, T. 1966 Grid turbulence at large Reynolds numbers. J. Fluid Mech. 26 (1), 37–47.Google Scholar
Kolmogorov, A. N. 1941 On the degeneration of isotropic turbulence in an incompressible viscous fluid [also in ‘Turbulence: Classical papers on statistical theory’, 1961, Friedlander S. K. and Topper L. (Eds.), Interscience]. Dokl. Akad. Nauk SSSR 31, 538–541.Google Scholar
Krogstad, P. Å & Davidson, P. A. 2010 Is grid turbulence Saffman turbulence?. J. Fluid Mech. 642, 373–394.Google Scholar
Krogstad, P. Å & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.Google Scholar
Larssen, J. V. & Devenport, W. J. 2002 The generation of high Reynolds number homogeneous turbulence. In Proceedings 32nd AIAA Fluid Dynamics Conference, Exhibit 2861. AIAA Inc.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Lavoie, P. 2006 Effects of initial conditions on decaying grid turbulence. Ph.D. Thesis, University of Newcastle, Newcastle, Australia.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Lee, S. K., Benaissa, A., Djenidi, L., Lavoie, P. & Antonia, R. A. 2012a Decay of passive-scalar fluctuations in slightly stretched grid turbulence. Exp. Fluids 53, 909–923.Google Scholar
Lee, S. K., Benaissa, A., Djenidi, L., Lavoie, P. & Antonia, R. A. 2012b Scaling range of velocity and passive scalar spectra in grid turbulence. Phys. Fluids 24, 075101.Google Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: EDQNM study. J. Turbul. 1 (7), 1–25.Google Scholar
Lesieur, M. & Schertzer, D. 1978 Amortissement auto-similaire d’une turbulence à grand nombre de Reynolds. J. Méc. 17, 609–646.Google Scholar
Llor, A. 2011 Langevin equation of big structure dynamics in turbulence: Landau’s invariant in the decay of homogeneous isotropic turbulence. Eur. J. Mech. B 30, 480–504.Google Scholar
Loitsyansky, L. G. 1939 Some basic laws for isotropic turbulent flow [1945 English translation in Natl. Advis. Comm. Aeronaut. Tech. Memo. 1079]. Trudy Tsentr. Aero.-Giedrodin Inst. 440, 3–23.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–64.Google Scholar
Mansour, N. N. & Wray, A. A. 1994 Decay of isotropic turbulence at low Reynolds number. Phys. Fluids 6 (2), 808–814.CrossRefGoogle Scholar
Moffat, R. J. 1988 Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1, 3–17.Google Scholar
Mohamed, M. S. & LaRue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics: Mechanics of Turbulence (vol. 2). MIT Press.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Péclet-number grid turbulence. J. Fluid Mech. 358, 135–175.Google Scholar
Proudman, I. & Reid, W. H. 1954 On the decay of a normally distributed and homogeneous turbulent velocity field. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 247 (926), 163–189.Google Scholar
Rey, C., Gence, J.-N., Schon, J.-P. & Mathieu, J. 1976 Étude de l’analogie entre champs thermiques et dynamique en turbulence homogène et isotrope dont les nombres de Péclet et de Reynolds sont petits, dans l’espace physique. C. R. Acad. Sci. (Paris) Ser. B 282, 79–82.Google Scholar
Ristorcelli, J. R. 2003 The self-preserving decay of isotropic turbulence: analytic solutions for energy and dissipation. Phys. Fluids 15 (10), 3248–3250.Google Scholar
Saffman, P. G. 1967a Note on decay of homogeneous turbulence. Phys. Fluids 10, 1349.Google Scholar
Saffman, P. G. 1967b The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27 (3), 581–593.Google Scholar
Schedvin, J., Stegen, G. R. & Gibson, C. H. 1974 Universal similarity at high grid Reynolds numbers. J. Fluid Mech. 66 (3), 561–579.CrossRefGoogle Scholar
Sirivat, A. & Warhaft, Z. 1983 The effect of a passive cross-stream temperature gradient on the evolution of temperature variance and heat flux in grid turbulence. J. Fluid Mech. 128, 323–346.Google Scholar
Speziale, C. G. & Bernard, P. S. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.CrossRefGoogle Scholar
Sreenivasan, K. R. 1984 On the scaling of the turbulence energy dissipation rate. Phys. Fluids 27 (5), 1048–1051.Google Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10 (2), 528–529.Google Scholar
Sreenivasan, K. R., Tavoularis, S., Henry, R. & Corrsin, S. 1980 Temperature fluctuations and scales in grid-generated turbulence. J. Fluid Mech. 100 (3), 597–621.CrossRefGoogle Scholar
Uberoi, M. S. 1956 Effect of wind-tunnel contraction on free stream turbulence. J. Aeronaut. Sci. 23 (8), 754–764.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Dependence of decaying homogeneous isotropic turbulence on inflow conditions. Phys. Lett. A 376, 510–514.Google Scholar
Vassilicos, J. C. 2011 An infinity of possible invariants for decaying homogeneous turbulence. Phys. Lett. A 375, 1010–1013.Google Scholar
Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.Google Scholar
Warhaft, Z. & Lumley, J. L. 1978 An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J. Fluid Mech. 88 (4), 659–684.Google Scholar
Wyngaard, J. C. 1968 Measurement of small-scale turbulence structure with hot wires. J. Sci. Instrum. (J. Phys. E) 1, 1105–1108.Google Scholar
Wyngaard, J. C. 1969 Spatial resolution of the vorticity meter and other hot-wire arrays. J. Sci. Instrum. (J. Phys. E) 2, 983–987.Google Scholar
Zhou, T., Antonia, R. A., Danaila, L. & Anselmet, F. 2000 Transport equations for the mean energy and temperature dissipation rates in grid turbulence. Exp. Fluids 28, 143–151.Google Scholar
Zhou, T., Antonia, R. A., Lasserre, J-J., Coantic, M. & Anselmet, F. 2003 Transverse velocity and temperature derivative measurements in grid turbulence. Exp. Fluids 34, 449–459.Google Scholar