Convection in a spherical shell is widely used to model fluid layers of planets and stars. The choice of thermal boundary conditions in such models is not always straightforward. To understand the implications of this choice, we report on the effects of the thermal boundary condition on thermal convection, in terms of instability onset, fully developed transport properties and flow structure. We impose a Robin boundary condition, enforcing linear coupling between the temperature anomaly and its radial derivative, with the Biot number 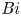${{\textit {Bi}}}$ as a proportionality factor in non-dimensional form. Varying 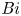${{\textit {Bi}}}$ allows us to transition from fixed temperature for 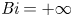${{\textit {Bi}}}=+\infty$, to imposed heat flux for 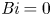${{\textit {Bi}}}=0$. We find that the onset of convection is only affected by 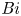${{\textit {Bi}}}$ in the non-rotating case. Far from onset, considering an effective Rayleigh number and a generalized Nusselt number, we show that the Nusselt and Péclet numbers follow standard universal scaling laws, independent of 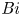${{\textit {Bi}}}$ in all cases considered. However, for the non-rotating limit, the large-scale flow structure keeps the signature of the boundary condition with more vigorous large scales for smaller 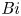${{\textit {Bi}}}$, even though the global heat transfer and kinetic energy are the same. For all practical purposes, the Robin condition can be safely replaced by a fixed flux when 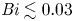${{\textit {Bi}}} \lesssim 0.03$ and by a fixed temperature for 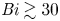${{\textit {Bi}}}\gtrsim 30$. For turbulent rapidly rotating convection, the thermal boundary condition does not seem to have any impact, once the effective numbers are considered and a reference temperature profile has been chosen.

Interaction of droplets with vortical structures is ubiquitous in nature, ranging from raindrops to a gas turbine combustor. In this work, we elucidate the mechanism of co-axial interaction of a droplet with a vortex ring of different circulation strengths ($\varGamma = 45\text {--}161\ \textrm {cm}^2\ \textrm {s}^{-1}$). We focus on both the droplet and the vortex dynamics, which evolve in a spatio-temporal fashion during different stages of the interaction, as in a two-way coupled system. Vortex rings of varying circulation strengths are generated by injecting a slug of water into a quiescent water-filled chamber. Experimental techniques such as high-speed particle image velocimetry, planner laser-induced fluorescence imaging and high-speed shadowgraphy are used in this work. In the droplet dynamics, different regimes of interaction are identified, including deformation (regime-I), stretching and engulfment (regime-II) and breakup of the droplet (regime-III). Each interaction regime is explained using existing theoretical models that closely match the experimental data. In the vortex dynamics, we compare the interaction's effect on different characteristics of the vortex rings, such as pressure and the vorticity distribution, circulation strength, total energy and enstrophy variation with time. It is found that the interaction leads to a reduction in these parameters.

The present work focuses on the study of the resonance and coupling of an underexpanded circular twin-jet system operating at a nozzle pressure ratio of $5.0$. Particle image velocimetry data from previous work were revisited, and a symmetry-imposed proper orthogonal decomposition (POD) was performed. It is shown that the system is dominated by a single POD mode pair symmetric about the internozzle plane, and the resonance loop is modulated by a third POD mode related to shear thickness modulation. A spatial Fourier transform of the leading POD mode pair leads to the identification of the peak wavenumbers and radial shapes of the different waves at play in the screech phenomenon. Locally parallel linear stability analysis around the experimental mean flow is also performed, in order to provide clarification of the mode ‘locking’ mechanism, i.e. the selection of the global mode associated with screech. It is shown that the characteristics of the Kelvin–Helmholtz wavepackets alone are not sufficient to explain the coupling observed in the experimental data. A consideration of the upstream-travelling guided jet mode offers an explanation; only specific symmetries of upstream modes can be supported in the frequency range at which resonance occurs. Results from stability analysis point to structures at frequencies and wavenumbers close to those found experimentally, and their spatial structures show excellent agreement with the POD modes. The present results suggest that the resonance loop is closed by an upstream-travelling guided jet mode for the twin-jet system at high nozzle pressure ratio.

Given the current lack of experimental data for shock waves interacting with incoming transitional boundary layers, the goal of this study was to characterize the dynamics of such an interaction to better understand the fundamental fluid physics of these complex phenomena. Here, the mean flow field and time-dependent characteristics of a three-dimensional Mach 5 cylinder-induced shock-wave/boundary-layer interaction where the upstream boundary layer is transitional, have been studied experimentally. The interactions were generated with a right circular cylinder mounted on a flat plate. Streamwise–spanwise planar laser scattering from a condensed alcohol fog and schlieren imaging were used to characterize the mean and instantaneous structure of the interaction, and fast-response wall-pressure measurements on the centreline upstream of the cylinder enabled characterization of the unsteadiness. The pressure measurements show a mean pressure profile that resembles a composite of an upstream laminar profile and a downstream turbulent profile. The upstream influence location of the transitional interaction was approximately 8.5 diameters ($d$) upstream of the cylinder leading edge, which is between that of a laminar and a turbulent interaction, and is followed by a plateau region to approximately $4d$ upstream of the cylinder. The plateau region is a region with a thicker boundary layer and possible flow separation. The plateau pressure was within 7 % of the value predicted by Hill's correlation for free-interaction phenomena. Furthermore, a statistical analysis of the pressure histories suggests that the entire interaction stretches and contracts in concert. Power spectral densities of the pressure fluctuations showed unsteadiness throughout the interaction with energy content primarily centred between a region defined by a separation-length-based Strouhal number $St_{L} = 0.05\text {--}0.2$, comparing well with other related studies of cylinder-induced interactions. Cross-correlations and coherence functions in the interaction suggest that the unsteadiness in the laminar region may be due to the entire ‘laminar’ region oscillating in response to the ‘turbulent’ unsteadiness of the intermittent region.

Smooth-walled open channel flow datasets, covering both the direct numerical simulation and experimental measurements with a friction Reynolds number ${\textit {Re}}_\tau$ at a low-to-moderate level of $550\sim 2400$, are adopted to investigate the contributions of different scale motions to the mean wall-shear stress in open channel flows (OCFs). The FIK identity decomposition method by Fukagata et al. (Phys. Fluids, vol. 14, 2002, L73) combined with a scale decomposition is chosen for this research. To see whether/how the contributions in OCFs differ with those in closed channel flows (CCFs), comparisons between the two flows are also made. The scale-decomposed ‘turbulent’ contribution results of present OCFs exhibit two dominant contribution modes (i.e. large-scale motions (LSMs) and very-large-scale motions (VLSMs)) at a streamwise wavelength $\lambda _x=1\sim 2h$ and $O(10h)$, where $h$ is the water depth. The large scales with $\lambda _x>3h$ and $\lambda _x>10h$ are demonstrated to contribute to over 40 % and 20 % of the mean wall-shear stress, respectively. Compared with CCFs, slightly higher and lower contributions in the $\lambda _x>O(10h)$ and $\lambda _x < O(10h)$ wavelength ranges are observed in OCFs, revealing the important free-surface effects in OCFs. Possible mechanisms are discussed to lend support for the observed differences between the two flows.

Trailing vortices typically persist into the extreme far-wake where the asymptotic perturbation dominates. In this work, we investigate the mechanism underlying the asymptotic growth of perturbation in trailing vortices by looking into the linear instabilities of two canonical trailing vortex systems, namely an isolated vortex and a co-rotating vortex pair with axial flow, generated by an M6 swept wing without/with winglets in a wind tunnel experiment. The dynamics and wandering phenomena of both vortex configurations are characterized by stereoscopic particle image velocimetry (SPIV). Their linear perturbation modes are acquired by local and bi-global linear stability analyses. For the isolated trailing vortex, the dominating perturbation mode is found to be a viscous, unstable Mode-A counter to the vortex rotation ($m>0$), while Mode-A with $m\leqslant 0$ is essentially damped and Mode-P, which is exclusive to $|m|\leqslant 1$, remains marginally stable. For the co-rotating vortex pair, the upper vortex is subject to an unstable, azimuthal perturbation, while the dominating perturbation of the lower vortex is radial. The perturbation mode of the upper vortex is more unstable than that of the lower vortex. The difference is supported by the corresponding wandering amplitude. The dominating modes of the two vortex configurations manifest an identical feature of azimuthal perturbations penetrating the core boundary. The dominating mode overwhelms those centre modes confined within the core. For both vortex configurations, a limiting penetration depth exists, where the perturbation is most amplified asymptotically. The limiting penetration depth is ascribed to the alignment of the critical point with vortex shear. For the isolated vortex, it is the shear layer at the core boundary; for the vortex pair, it is the mutual shear layer of both vortices. The asymptotic growth of perturbations is thus attributed to an interaction between the respective characteristic layers of the perturbation and the flow at the leading order.

We study the flow past a cylinder whose axis undergoes prescribed oscillations, translating uniformly in a direction transverse to the oncoming flow. We consider modest Reynolds numbers ($Re\leq 100$), for which the flow is two-dimensional; when the cylinder is fixed, vortices are shed periodically in a so-called 2S pattern. We choose the period of the prescribed oscillation to be identical to the period of the vortex shedding for a fixed cylinder. At a fixed Reynolds number of $Re=100$, an increase in the amplitude of the oscillations leads to a change in the topology of the shed vortices: the 2S pattern becomes a P+S pattern. We employ a space–time discretisation to directly compute time-periodic solutions of the Navier–Stokes equations and thus demonstrate that the transition between the two vortex shedding patterns arises through a spatio-temporal symmetry-breaking bifurcation of the time-periodic 2S solution. The P+S solution exists only for a finite range of amplitudes, however, and eventually reconnects with the 2S solution branch via a second symmetry-breaking bifurcation. There are ranges of amplitudes over which the system is bistable and both 2S and P+S could, in principle, be seen in experiments. As the Reynolds number is reduced, the 2S and P+S branches disconnect, but a bistable region remains until the isolated P+S solutions ultimately disappear, leaving only the 2S solution. The inferred stability of the various time-periodic solution branches is confirmed through time integration of the Navier–Stokes equations. Finally, we illustrate the evolution of the vorticity field along the solution branches.

This study examines the influence of flow nonlinearity in western boundary layers upon the turbulent wind-driven ocean gyres. Our analysis involves comparisons between large-scale circulation properties of the linear and nonlinear states, as well as a Lagrangian particle analysis of relevant flow features. We find that the so-called counter-rotating gyre anomalies, which are nonlinear circulation features embedded in the gyres, are consistent in shape with the linear, weakened, wind-curl response created by the geometric wind effect. However, the linear response is far too weak without considering nonlinear effects. Within the western boundary layer lobe of these features, the nonlinear boundary layer has a pivotal impact upon the global circulation. Effects of potential vorticity advection inhibit viscous relative vorticity fluxes through the western boundary. This creates a significant potential vorticity imbalance between the gyres. Consequently, this generates an accumulation of enstrophy downstream in the inertial recirculation zones, which in turn supports the eastward jet. However, within the ocean basin, the growing imbalance is eventually rectified by inter-gyre potential vorticity exchanges owing to nonlinear fluxes. The Lagrangian particle analysis reveals the inter-gyre exchange mechanism, where particles seeded within the western boundary layer migrate between the gyres and weaken the eastward jet extension.

Phase-averaged and cycle-to-cycle analysis of key contributors to sound production in phonation is examined in a scaled-up vocal-fold model. Simultaneous temporally and spatially resolved pressure and velocity measurements permitted examination of each term in the streamwise integral momentum equation. The relative sizes of these terms were used to address the issue of whether transglottal pressure is a surrogate for vocal-fold drag, a quantity directly related to sound production. Further, time traces of transglottal pressure and volume flow rate provided insight into the role of cycle-to-cycle variations in voiced sound production which affect voice quality. Experiments were conducted using a 10× scaled-up model in a free-surface water tunnel. Two-dimensional vocal-fold models with semi-circular ends inside a square duct were driven with constant opening and closing speeds. The time from opening to closed, To, was half the oscillation period. Time-resolved digital particle image velocimetry (DPIV) and pressure measurements along the duct centreline were made for 3650 ≤ Re ≤ 8100 and equivalent life frequencies from 52.5 to 97.5 Hz. Results showed that transglottal pressure does serve as a surrogate for the vocal-fold drag. However, smaller but non-negligible momentum flux and inertia terms, caused by the jet and vocal-fold motions, may also contribute to vocal-fold drag. Further, cycle-to-cycle variations including jet switching and modulation are inherent in flows of this type despite their high degrees of symmetry and repeatability. The origins of these variations and their potential role in sound production and voice quality are discussed.

Aquatic locomotion of a deformable body from rest up to its asymptotic speed is given by the unsteady motion which is produced by a series of periodic reactions dictated by the body configuration and by the style of swimming. The added mass plays a crucial role, not only for the initial burst, but also along each manoeuvre, to accelerate the surrounding fluid for generating the kinetic energy and to enable vortex shedding in the wake. The estimate of these physical aspects has been largely considered in most theoretical models, but not sufficiently deepened in many experimental and numerical investigations. As a motivation, while the vortical structures are easily detectable from the flow field, the added mass, on the contrary, is usually embedded in the overall forcing terms. By the present impulse formulation, we are able to separate and to emphasize the role of the added mass and vorticity release to evaluate in a neat way their specific contributions. The precise identification of the added mass is also instrumental for a well-posed numerical problem and for easily readable results. As a further point, the asymptotic speed is found to be guided either by the phase velocity of the prescribed undulation and by the unavoidable recoil motion induced by the self-propelled swimming. The numerical results reported in the present paper concern simplified cases of non-diffusing vorticity and two-dimensional flow.

The well-known two-dimensional problem of a plane acoustic wave scattering by a point vortex is ill-posed because the vortex velocity field decays as $r^{-1}$ at infinity. We show that for problem to be well-posed, the velocity field must decay more rapidly than as $r^{-3/2}$. We propose a reformulation where the point vortex is screened by a vortical mantle with the opposite total circulation such that the velocity field is proportional to $r^{-1} \exp (-r^2 / L^2)$. The vortex effective radius $L$ is assumed long compared with the acoustic wavelength $\lambda$. In the Born approximation, the scattered field is the solution to the inhomogeneous Helmholtz equation with the Sommerfeld radiation condition that can be represented as convolution of the source term with Green's function. The asymptotic evaluation as $\lambda / L \to 0$ shows the analogy to plane-wave diffraction by a slit of width $L$. In the Fraunhofer region $r \gg L^2 / \lambda$, the solution is an outgoing cylindrical wave that peaks at small scattering angles $\theta = O(\lambda / L)$ and matches the expression with a singularity on $\theta = 0$ known from the case of the point vortex (Pitaevskii, Sov. Phys. JETP, vol. 8, 1959, pp. 888–890) as $\theta \gg \lambda / L$. In a part of the region of geometrical acoustics $r \ll L^2 / \lambda$ including the region $r \ll L$ where the vortex velocity field is proportional to $r^{-1}$, the solution matches the second known expression (Sakov, Acoust. Phys., vol. 39, 1993, pp. 280–282) that does not decay at infinity. The results are confirmed by numerical integration.

A novel flow instability emerging during a rheometric flow of a phase change material sheared in the vicinity of the melting point is reported. Right above the onset of the flow-induced crystallisation, the presence of the crystals in the flow leads to a primary bifurcation towards an oscillatory flow state. A further decrease of the temperature beyond this point leads to an increase of both the volume fraction and the size of the crystals, which ultimately triggers a fully developed chaotic flow. A full stability diagram as a function of the imposed deformation rate and the temperature is obtained experimentally. The systematic experimental observations reported herein could trigger further studies of the hydrodynamics of phase change materials and may find a number of interesting applications in polymer processing and thermal storage. The experimental findings are complemented by the analysis of a simple numerical model which provides further insights into the physical origins and mechanism of the instability.