We present direct numerical simulation of a mechanism for creating longitudinal vortices in pipe flow, compared with a model theory. By furnishing the pipe wall with a pattern of crossing waves, secondary flow in the form of streamwise vortex pairs is created. The mechanism, ‘CL1’, is kinematic and known from oceanography as a driver of Langmuir circulation. CL1 is strongest when the ‘wall wave’ vectors make an acute angle with the axis, 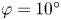 $\varphi =10^{\circ }$–
$\varphi =10^{\circ }$–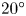 $20^{\circ }$, changes sign near
$20^{\circ }$, changes sign near 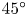 $45^{\circ }$ and is weak and of opposite sign beyond this angle. A competing, dynamic mechanism driving secondary flow in the opposite sense is also observed, created by the azimuthally varying friction. Whereas at smaller angles ‘CL1’ prevails, the dynamic effect dominates when
$45^{\circ }$ and is weak and of opposite sign beyond this angle. A competing, dynamic mechanism driving secondary flow in the opposite sense is also observed, created by the azimuthally varying friction. Whereas at smaller angles ‘CL1’ prevails, the dynamic effect dominates when 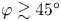 $\varphi \gtrsim 45^{\circ }$, reversing the flow. Curiously, the circulation strength is a faster-than-linearly increasing function of Reynolds number for small
$\varphi \gtrsim 45^{\circ }$, reversing the flow. Curiously, the circulation strength is a faster-than-linearly increasing function of Reynolds number for small  $\varphi$. We explore an analogy with Prandtl's secondary motion of the second kind in turbulence. A transport equation for average streamwise vorticity is derived, and we analyse it for three different crossing angles,
$\varphi$. We explore an analogy with Prandtl's secondary motion of the second kind in turbulence. A transport equation for average streamwise vorticity is derived, and we analyse it for three different crossing angles, 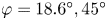 $\varphi =18.6^{\circ }, 45^{\circ }$ and
$\varphi =18.6^{\circ }, 45^{\circ }$ and 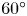 $60^{\circ }$. Mean-vorticity production is organised in a ring-like structure with the two rings contributing to rotating flow in opposite senses. For the larger
$60^{\circ }$. Mean-vorticity production is organised in a ring-like structure with the two rings contributing to rotating flow in opposite senses. For the larger 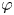 $\varphi$, the inner ring decides the main swirling motion, whereas for
$\varphi$, the inner ring decides the main swirling motion, whereas for 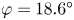 $\varphi =18.6^{\circ }$, outer-ring production dominates. For the larger angles, the outer ring is mainly driven by advection of vorticity and the inner by deformation (stretching) whereas, for
$\varphi =18.6^{\circ }$, outer-ring production dominates. For the larger angles, the outer ring is mainly driven by advection of vorticity and the inner by deformation (stretching) whereas, for 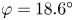 $\varphi =18.6^{\circ }$, both contribute approximately equally to production in the outer ring.
$\varphi =18.6^{\circ }$, both contribute approximately equally to production in the outer ring.