Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gan, Yanbiao
Xu, Aiguo
Lai, Huilin
Li, Wei
Sun, Guanglan
and
Succi, Sauro
2022.
Discrete Boltzmann multi-scale modelling of non-equilibrium multiphase flows.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Zhu, Yi
Pang, Jian-Hua
and
Tian, Fang-Bao
2022.
Point-to-Point Navigation of a Fish-Like Swimmer in a Vortical Flow With Deep Reinforcement Learning.
Frontiers in Physics,
Vol. 10,
Issue. ,
Kumar, Kamlesh
and
Prabhakaran, Deepu
2022.
Nonlinear oscillations of a collapsible tube subjected to unsteady external pressure.
Physics of Fluids,
Vol. 34,
Issue. 6,
Ji, Xueyu
Wang, Li
Ravi, Sridhar
Tian, Fang-Bao
Young, John
and
Lai, Joseph C. S.
2022.
Influences of serrated trailing edge on the aerodynamic and aeroacoustic performance of a flapping wing during hovering flight.
Physics of Fluids,
Vol. 34,
Issue. 1,
Zhao, Wenhan
Wu, Wenshuai
Yuan, Dan
Zou, Siyuan
Yang, Fan
Zhao, Qianbin
Mehmood, Kashif
and
Zhang, Boran
2022.
Experimental exploration on stable expansion phenomenon of sheath flow in viscous microfluidics.
Physics of Fluids,
Vol. 34,
Issue. 12,
Wang, Li
Dong, Daoyi
and
Tian, Fang-Bao
2022.
Fast prediction of blood flow in stenosed arteries using machine learning and immersed boundary-lattice Boltzmann method.
Frontiers in Physiology,
Vol. 13,
Issue. ,
Huang, Qiuxiang
Liu, Zhengliang
Wang, Li
Ravi, Sridhar
Young, John
Lai, Joseph C. S.
and
Tian, Fang-Bao
2022.
Streamline penetration, velocity error, and consequences of the feedback immersed boundary method.
Physics of Fluids,
Vol. 34,
Issue. 9,
Huang, Qiuxiang
Bhat, Shantanu S.
Yeo, Eng Chow
Young, John
Lai, Joseph C.S.
Tian, Fang-Bao
and
Ravi, Sridhar
2023.
Power synchronisations determine the hovering flight efficiency of passively pitching flapping wings.
Journal of Fluid Mechanics,
Vol. 974,
Issue. ,
Zhu, Yi
Pang, Jian-Hua
Gao, Tong
and
Tian, Fang-Bao
2023.
Learning to school in dense configurations with multi-agent deep reinforcement learning.
Bioinspiration & Biomimetics,
Vol. 18,
Issue. 1,
p.
015003.
Shan, Yiming
Xu, Aiguo
Zhang, Yudong
Wang, Lifeng
and
Chen, Feng
2023.
Discrete Boltzmann modeling of detonation: Based on the Shakhov model.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 237,
Issue. 11,
p.
2517.
Liu, Zhipeng
Song, Jiahui
Xu, Aiguo
Zhang, Yudong
and
Xie, Kan
2023.
Discrete Boltzmann modeling of plasma shock wave.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 237,
Issue. 11,
p.
2532.
Wang, Li
Liu, Zhengliang
and
Rajamuni, Methma
2023.
Recent progress of lattice Boltzmann method and its applications in fluid-structure interaction.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 237,
Issue. 11,
p.
2461.
Huang, Qiuxiang
Tian, Fang-Bao
Young, John
Lai, Joseph
and
Ravi, Sridhar
2023.
Numerical Study of Passively Pitching Tandem Dragonfly Wings for Hovering Flight.
Liu, Zhengliang
Huang, Qiuxiang
Li, Zongjun
Li, Ye
and
Feng, Xingya
2023.
Partial confinement effects on the performance of a flapping foil power generator.
Physics of Fluids,
Vol. 35,
Issue. 2,
Huang, Qiuxiang
Kou, Jiaqing
Tian, Fang-Bao
Young, John
Lai, Joseph
and
Ravi, Sridhar
2023.
Dynamic Mode Decomposition for Unsteady Flow over Flapping Wings.
Mazharmanesh, Soudeh
Tian, Fang-Bao
and
Lei, Chengwang
2023.
Enhancing heat transfer using flow-induced oscillations of a flexible baffle attached to a vertical heated flat surface.
International Journal of Thermal Sciences,
Vol. 194,
Issue. ,
p.
108604.
Ma, Jingtao
Huang, Qiuxiang
Zhu, Yi
Xu, Yuan-Qing
and
Tian, Fang-Bao
2023.
Effects of fluid rheology on dynamics of a capsule through a microchannel constriction.
Physics of Fluids,
Vol. 35,
Issue. 9,
Cui, Jingyu
Wang, Zhaokun
Ren, Feng
Liu, Yang
Yan, Weiwei
and
Jin, Yuzhen
2024.
Buckled elastic sheet as a vortex generator in dual channels.
Journal of Fluid Mechanics,
Vol. 985,
Issue. ,
Qin, Jianhua
Liao, Fei
Dong, Guodan
and
Yang, Xiaolei
2024.
Parallelization strategies for resolved simulations of fluid-structure-particle interactions.
Applied Mathematics and Mechanics,
Vol. 45,
Issue. 5,
p.
857.
Huang, Qiuxiang
Ji, Xueyu
Ma, Jingtao
Wang, Li
Young, John
and
Lai, Joseph C. S.
2024.
Self-excited oscillations of three-dimensional collapsible tubes conveying both laminar and turbulent flows.
Physics of Fluids,
Vol. 36,
Issue. 12,
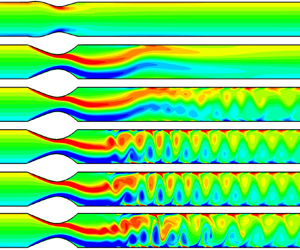
 $Re$, structure-to-fluid mass ratios
$Re$, structure-to-fluid mass ratios  $M$ and external pressures
$M$ and external pressures  $P_e$. Based on extensive simulations, we first characterise the chaotic behaviours of the collapsible channel flow and explore possible routes to chaos. We then explore the physical mechanisms responsible for the onset of self-excited oscillations. Nonlinear and rich dynamic behaviours of the collapsible system are discovered. Specifically, the system experiences a supercritical Hopf bifurcation leading to a period-1 limit cycle oscillation. The existence of chaotic behaviours of the collapsible channel walls is confirmed by a positive dominant Lyapunov exponent and a chaotic attractor in the velocity-displacement phase portrait of the mid-point of the collapsible channel wall. Chaos in the system can be reached via period-doubling and quasi-periodic bifurcations. It is also found that symmetry breaking is not a prerequisite for the onset of self-excited oscillations. However, symmetry breaking induced by mass ratio and external pressure may lead to a chaotic state. Unbalanced transmural pressure, wall inertia and shear layer instabilities in the vorticity waves contribute to the onset of self-excited oscillations of the collapsible system. The period-doubling, quasi-periodic and chaotic oscillations are closely associated with vortex pairing and merging of adjacent vortices, and interactions between the vortices on the upper and lower walls downstream of the throat.
$P_e$. Based on extensive simulations, we first characterise the chaotic behaviours of the collapsible channel flow and explore possible routes to chaos. We then explore the physical mechanisms responsible for the onset of self-excited oscillations. Nonlinear and rich dynamic behaviours of the collapsible system are discovered. Specifically, the system experiences a supercritical Hopf bifurcation leading to a period-1 limit cycle oscillation. The existence of chaotic behaviours of the collapsible channel walls is confirmed by a positive dominant Lyapunov exponent and a chaotic attractor in the velocity-displacement phase portrait of the mid-point of the collapsible channel wall. Chaos in the system can be reached via period-doubling and quasi-periodic bifurcations. It is also found that symmetry breaking is not a prerequisite for the onset of self-excited oscillations. However, symmetry breaking induced by mass ratio and external pressure may lead to a chaotic state. Unbalanced transmural pressure, wall inertia and shear layer instabilities in the vorticity waves contribute to the onset of self-excited oscillations of the collapsible system. The period-doubling, quasi-periodic and chaotic oscillations are closely associated with vortex pairing and merging of adjacent vortices, and interactions between the vortices on the upper and lower walls downstream of the throat.