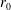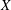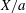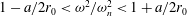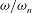A novel reduced-order model for time-varying nonlinear flows arising from a resolvent decomposition based on the time-mean flow is proposed. The inputs required for the model are the mean-flow field and a small set of velocity time-series data obtained at isolated measurement points, which are used to fix relevant frequencies, amplitudes and phases of a limited number of resolvent modes that, together with the mean flow, constitute the reduced-order model. The technique is applied to derive a model for the unsteady three-dimensional flow in a lid-driven cavity at a Reynolds number of 1200 that is based on the two-dimensional mean flow, three resolvent modes selected at the most active spanwise wavenumber, and either one or two velocity probe signals. The least-squares full-field error of the reconstructed velocity obtained using the model and two point velocity probes is of the order of 5 % of the lid velocity, and the dynamical behaviour of the reconstructed flow is qualitatively similar to that of the complete flow.

A submerged body subject to a sudden shape change experiences large forces due to the variation of added-mass energy. While this phenomenon has been studied for single actuation events, application to sustained propulsion requires the study of periodic shape change. We do so in this work by investigating a spring–mass oscillator submerged in quiescent fluid subject to periodic changes in its volume. We develop an analytical model to investigate the relationship between added-mass variation and viscous damping, and demonstrate its range of application with fully coupled fluid–solid Navier–Stokes simulations at large Stokes number. Our results demonstrate that the recovery of added-mass kinetic energy can be used to completely cancel the viscous damping of the fluid, driving the onset of sustained oscillations with amplitudes as large as four times the average body radius $r_{0}$. A quasi-linear relationship is found to link the terminal amplitude of the oscillations $X$ to the extent of size change $a$, with $X/a$ peaking at values from 4 to 4.75 depending on the details of the shape-change kinematics. In addition, it is found that pumping in the frequency range of $1-a/2r_{0}<{\it\omega}^{2}/{\it\omega}_{n}^{2}<1+a/2r_{0}$, with ${\it\omega}/{\it\omega}_{n}$ being the ratio between frequency of actuation and natural frequency, is required for sustained oscillations. The results of this analysis shed light on the role of added-mass recovery in the context of shape-changing bodies and biologically inspired underwater vehicles.