Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T17:40:35.583Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag cancellation by added-mass pumping

Published online by Cambridge University Press:  08 June 2016

F. Giorgio-Serchi  and
G. D. Weymouth
F. Giorgio-Serchi*
Affiliation:
Southampton Marine and Maritime Institute, Fluid Structure Interaction Group, University of Southampton, Southampton SO16 7QF, UK
G. D. Weymouth
Affiliation:
Southampton Marine and Maritime Institute, Fluid Structure Interaction Group, University of Southampton, Southampton SO16 7QF, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A submerged body subject to a sudden shape change experiences large forces due to the variation of added-mass energy. While this phenomenon has been studied for single actuation events, application to sustained propulsion requires the study of periodic shape change. We do so in this work by investigating a spring–mass oscillator submerged in quiescent fluid subject to periodic changes in its volume. We develop an analytical model to investigate the relationship between added-mass variation and viscous damping, and demonstrate its range of application with fully coupled fluid–solid Navier–Stokes simulations at large Stokes number. 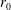Our results demonstrate that the recovery of added-mass kinetic energy can be used to completely cancel the viscous damping of the fluid, driving the onset of sustained oscillations with amplitudes as large as four times the average body radius $r_{0}$. A quasi-linear relationship is found to link the terminal amplitude of the oscillations 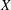$X$ to the extent of size change $a$, with 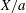$X/a$ peaking at values from 4 to 4.75 depending on the details of the shape-change kinematics. In addition, it is found that pumping in the frequency range of 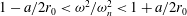$1-a/2r_{0}<{\it\omega}^{2}/{\it\omega}_{n}^{2}<1+a/2r_{0}$, with 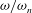${\it\omega}/{\it\omega}_{n}$ being the ratio between frequency of actuation and natural frequency, is required for sustained oscillations. The results of this analysis shed light on the role of added-mass recovery in the context of shape-changing bodies and biologically inspired underwater vehicles.

JFM classification

Flow Control: Drag reduction Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , R3
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Candelier, F., Boyer, F. & Leroyer, A. 2011 Three-dimensional extension of Lighthill’s large-amplitude elongated-body theory of fish locomotion. J. Fluid Mech. 674, 196–226.Google Scholar
Daniel, T. L. 1984 Unsteady aspects of aquatic locomotion. Am. Zool. 24 (1), 121–134.Google Scholar
Daniel, T. L. 1985 Cost of locomotion: unsteady medusan swimming. J. Exp. Biol. 119, 149–164.CrossRefGoogle Scholar
Giorgio-Serchi, F., Arienti, A. & Laschi, C. 2016 Underwater soft-bodied pulsed-jet thrusters: actuator modeling and performance profiling. Intl J. Robot. Res. (to appear) doi:10.1177/0278364915622569.Google Scholar
Johnson, W., Soden, P. D. & Trueman, E. R. 1972 A study in met propulsion: an analysis of the motion of the squid, Loligo Vulgaris . J. Exp. Biol. 56, 155–165.Google Scholar
Kanso, E. 2009 Swimming due to transverse shape deformations. J. Fluid Mech. 631, 127–148.Google Scholar
Kanso, E. & Newton, P. K. 2009 Passive locomotion via normal-mode coupling in a submerged spring–mass system. J. Fluid Mech. 641, 201–215.Google Scholar
Lavroskii, E. K. & Formal’skii, A. M. 1993 Optimal control of the pumping and damping of a swing. Z. Angew. Math. Mech. 57, 311–320.CrossRefGoogle Scholar
Lighthill, M. J. 1960 Note on the swimming of slender fish. J. Fluid Mech. 9, 305–317.Google Scholar
Maertens, A. P. & Weymouth, G. D. 2015 Accurate Cartesian-grid simulations of near-body flows at intermediate Reynolds numbers. J. Comput. Phys. 283, 106–129.Google Scholar
Mei, R. 1994 Flow due to an oscillating sphere and an expression for unsteady drag on the sphere at finite Reynolds number. J. Fluid Mech. 270, 133–174.CrossRefGoogle Scholar
Morison, J. R., O’Brien, M. P., Johnson, J. W. & Schaaf, S. A. 1950 The force exerted by surface waves on piles. Petrol. Trans. AIME 189, 149–154.Google Scholar
Roura, P. & Gonzalez, J. A. 2010 Towards a more realistic description of swing pumping due to the exchange of angular momentum. Eur. J. Phys. 31, 1195–1207.Google Scholar
Saffman, P. G. 1967 The self-propulsion of a deformable body in a perfect fluid. J. Fluid Mech. 28, 385–389.Google Scholar
Spagnolie, S. E. & Shelley, M. J. 2009 Shape-changing bodies in fluids: hovering, ratcheting and bursting. Phys. Fluids 21, 1–13.Google Scholar
Trueman, E. R. & Packard, A. 1968 Motor performances of some cephalopods. J. Exp. Biol. 49, 495–507.Google Scholar
Weymouth, G. D., Subramaniam, V. & Triantafyllou, M. S. 2015 Ultra-fast escape maneuver of an octopus-inspired robot. Bioinsp. Biomimet. 10, 1–7.Google Scholar
Weymouth, G. D. & Triantafyllou, M. S. 2013 Ultra-fast escape of a deformable jet-propelled body. J. Fluid Mech. 721, 367–385.Google Scholar
Weymouth, G. D. & Yue, D. K.-P. 2011 Boundary data immersion method for Cartesian-grid simulations of fluid–body interaction problems. J. Comput. Phys. 230, 6233–6247.CrossRefGoogle Scholar

Giorgio-Serchi et al. supplemenatary movie

Evolution of the λ2 vortex criterion after attainment of zero-damping regime in response to the sharp and smooth radius variation profiles.

Download Giorgio-Serchi et al. supplemenatary movie(Video)
Video 23.2 MB