Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 198
Nonlinear self-excited thermoacoustic oscillations: intermittency and flame blowout
-
- Published online by Cambridge University Press:
- 17 October 2012, pp. 376-397
-
- Article
- Export citation
- Cited by 197
Shear-layer pressure fluctuations and superdirective acoustic sources
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 355-368
-
- Article
- Export citation
- Cited by 197
The Stokes flow problem for a class of axially symmetric bodies
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 529-549
-
- Article
- Export citation
- Cited by 197
The threefold classification of unstable disturbances in flexible surfaces bounding inviscid flows
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 436-450
-
- Article
- Export citation
- Cited by 197
Wall-induced forces on a rigid sphere at finite Reynolds number
-
- Published online by Cambridge University Press:
- 26 July 2005, pp. 1-25
-
- Article
- Export citation
- Cited by 197
Some observations of the vortex breakdown phenomenon
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 585-592
-
- Article
- Export citation
- Cited by 197
Linear-eddy modelling of turbulent transport. Part 6. Microstructure of diffusive scalar mixing fields
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 361-394
-
- Article
- Export citation
- Cited by 197
Velocity statistics in turbulent channel flow up to
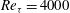 $Re_{\tau }=4000$
$Re_{\tau }=4000$
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 171-191
-
- Article
- Export citation
- Cited by 197
Entrainment and mixing in stratified shear flows
-
- Published online by Cambridge University Press:
- 13 February 2001, pp. 349-386
-
- Article
- Export citation
- Cited by 197
Internal solitary wave breaking and run-up on a uniform slope
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 133-154
-
- Article
- Export citation
- Cited by 197
Lateral dispersion in random cylinder arrays at high Reynolds number
-
- Published online by Cambridge University Press:
- 26 March 2008, pp. 339-371
-
- Article
- Export citation
- Cited by 197
The role of particle collisions in pneumatic transport
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 345-359
-
- Article
- Export citation
- Cited by 196
Fluid–structure interaction of a square cylinder at different angles of attack
-
- Published online by Cambridge University Press:
- 23 April 2014, pp. 688-721
-
- Article
- Export citation
- Cited by 196
Maximal two-layer exchange through a contraction with barotropic net flow
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 27-51
-
- Article
- Export citation
- Cited by 196
A stochastic model of two-particle dispersion and concentration fluctuations in homogeneous turbulence
-
- Published online by Cambridge University Press:
- 19 April 2006, pp. 279-302
-
- Article
- Export citation
- Cited by 196
Axisymmetric superdirectivity in subsonic jets
-
- Published online by Cambridge University Press:
- 03 July 2012, pp. 388-420
-
- Article
- Export citation
- Cited by 196
Deformation and breakup of a single slender drop in an extensional flow
-
- Published online by Cambridge University Press:
- 12 April 2006, pp. 641-672
-
- Article
- Export citation
- Cited by 196
Timescale and structure of ejections and bursts in turbulent channel flows
-
- Published online by Cambridge University Press:
- 21 April 2006, pp. 529-552
-
- Article
- Export citation
- Cited by 196
Lift and the leading-edge vortex
-
- Published online by Cambridge University Press:
- 27 February 2013, pp. 280-313
-
- Article
- Export citation
- Cited by 196
Local energy flux and subgrid-scale statistics in three-dimensional turbulence
-
- Published online by Cambridge University Press:
- 10 July 1998, pp. 1-31
-
- Article
- Export citation

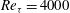
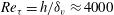
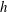
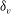
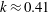

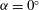
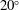
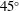

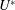
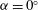
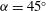
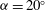
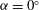
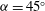
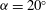

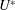

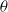 , was progressively varied, allows the decomposition of the acoustic pressure into azimuthal Fourier modes. In agreement with past observations, the sound field for low polar angles (measured with respect to the jet axis) is found to be dominated by the axisymmetric mode, particularly at the peak Strouhal number. The axisymmetric mode of the acoustic field can be clearly associated with an axially non-compact source, in the form of a wavepacket: the sound pressure level for peak frequencies is found be superdirective for all Mach numbers considered, with exponential decay as a function of
, was progressively varied, allows the decomposition of the acoustic pressure into azimuthal Fourier modes. In agreement with past observations, the sound field for low polar angles (measured with respect to the jet axis) is found to be dominated by the axisymmetric mode, particularly at the peak Strouhal number. The axisymmetric mode of the acoustic field can be clearly associated with an axially non-compact source, in the form of a wavepacket: the sound pressure level for peak frequencies is found be superdirective for all Mach numbers considered, with exponential decay as a function of 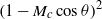 , where
, where 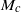 is the Mach number based on the phase velocity
is the Mach number based on the phase velocity 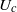 of the convected wave. While the mode
of the convected wave. While the mode 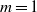 spectrum scales with Strouhal number, suggesting that its energy content is associated with turbulence scales, the axisymmetric mode scales with Helmholtz number – the ratio between source length scale and acoustic wavelength. The axisymmetric radiation has a stronger velocity dependence than the higher-order azimuthal modes, again in agreement with predictions of wavepacket models. We estimate the axial extent of the source of the axisymmetric component of the sound field to be of the order of six to eight jet diameters. This estimate is obtained in two different ways, using, respectively, the directivity shape and the velocity exponent of the sound radiation. The analysis furthermore shows that compressibility plays a significant role in the wavepacket dynamics, even at this low Mach number. Velocity fluctuations on the jet centreline are reduced as the Mach number is increased, an effect that must be accounted for in order to obtain a correct estimation of the velocity dependence of sound radiation. Finally, the higher-order azimuthal modes of the sound field are considered, and a model for the low-angle sound radiation by helical wavepackets is developed. The measured sound for azimuthal modes 1 and 2 at low Strouhal numbers is seen to correspond closely to the predicted directivity shapes.
spectrum scales with Strouhal number, suggesting that its energy content is associated with turbulence scales, the axisymmetric mode scales with Helmholtz number – the ratio between source length scale and acoustic wavelength. The axisymmetric radiation has a stronger velocity dependence than the higher-order azimuthal modes, again in agreement with predictions of wavepacket models. We estimate the axial extent of the source of the axisymmetric component of the sound field to be of the order of six to eight jet diameters. This estimate is obtained in two different ways, using, respectively, the directivity shape and the velocity exponent of the sound radiation. The analysis furthermore shows that compressibility plays a significant role in the wavepacket dynamics, even at this low Mach number. Velocity fluctuations on the jet centreline are reduced as the Mach number is increased, an effect that must be accounted for in order to obtain a correct estimation of the velocity dependence of sound radiation. Finally, the higher-order azimuthal modes of the sound field are considered, and a model for the low-angle sound radiation by helical wavepackets is developed. The measured sound for azimuthal modes 1 and 2 at low Strouhal numbers is seen to correspond closely to the predicted directivity shapes.