Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 1
Excitation and evolution of radiating modes in supersonic boundary layers. Part 2. Back effect of spontaneously radiated Mach waves
-
- Published online by Cambridge University Press:
- 18 April 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Mechanisms of mass transfer to small spheres sinking in turbulence
-
- Published online by Cambridge University Press:
- 03 January 2023, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Surfactant-laden film lining an oscillating cap: problem formulation and weakly nonlinear analysis
-
- Published online by Cambridge University Press:
- 05 July 2022, A50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Self-tuning model predictive control for wake flows
-
- Published online by Cambridge University Press:
- 18 March 2024, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Limiting regimes of turbulent horizontal convection. Part 2. Large Prandtl numbers
-
- Published online by Cambridge University Press:
- 21 October 2024, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
An asymptotic theory for the propagation of a surface-catalysed flame in a tube
-
- Published online by Cambridge University Press:
- 21 December 2005, pp. 363-393
-
- Article
- Export citation
- Cited by 1
Non-Hermitian Chern number in rotating Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 15 November 2024, A65
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
Relative fluid stretching and rotation for sparse trajectory observations
-
- Published online by Cambridge University Press:
- 03 October 2024, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Inviscid linear stability analysis of two vertical columns of different densities in a gravitational acceleration field
-
- Published online by Cambridge University Press:
- 09 August 2017, R4
-
- Article
- Export citation
- Cited by 1
Dynamics of the interaction of a pair of thin evaporating droplets on compliant substrates
-
- Published online by Cambridge University Press:
- 27 December 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Multiscale modelling and simulation of coexisting turbulent and rarefied gas flows
-
- Published online by Cambridge University Press:
- 26 December 2024, A10
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
A ‘reciprocal’ theorem for the prediction of loads on a body moving in an inhomogeneous flow at arbitrary Reynolds number – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 05 December 2011, pp. 605-606
-
- Article
-
- You have access
- Export citation
- Cited by 1
Asymmetry of motion: vortex rings crossing a density gradient
-
- Published online by Cambridge University Press:
- 30 March 2023, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
Stability of obliquely driven cavity flow
-
- Published online by Cambridge University Press:
- 11 October 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
The initial-value problem for three-dimensional disturbances in plane Poiseuille flow of helium II
-
- Published online by Cambridge University Press:
- 25 February 2008, pp. 227-244
-
- Article
- Export citation
- Cited by 1
FLM volume 897 Cover and Front matter
-
- Published online by Cambridge University Press:
- 29 June 2020, p. f1
-
- Article
-
- You have access
- Export citation
- Cited by 1
Exact Riemann solver for non-convex relativistic hydrodynamics
-
- Published online by Cambridge University Press:
- 22 November 2023, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 1
PROFESSOR PAUL H. STEEN 22 July 1952 – 4 September 2020
-
- Published online by Cambridge University Press:
- 05 January 2021, E1
-
- Article
-
- You have access
- HTML
- Export citation
- Cited by 1
Interfacial pattern selection in defiance of linear growth
-
- Published online by Cambridge University Press:
- 19 September 2017, pp. 345-363
-
- Article
- Export citation
- Cited by 1
On the origin of counter-gradient transport in turbulent scalar flux: physics interpretation and adjoint data assimilation
-
- Published online by Cambridge University Press:
- 19 November 2024, A81
-
- Article
-
- You have access
- HTML
- Export citation

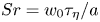
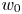
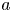
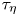
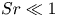
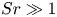
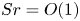
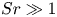






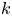
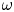
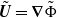 , to (E.6) which holds for any velocity
, to (E.6) which holds for any velocity 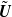 , an extra term
, an extra term 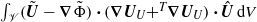 arises on the right-hand side of the latter and hence on that of (E.8). Therefore the right-hand side of (3.6) actually involves an additional contribution
arises on the right-hand side of the latter and hence on that of (E.8). Therefore the right-hand side of (3.6) actually involves an additional contribution 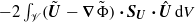 , where
, where 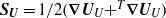 denotes the strain-rate tensor associated with the undisturbed flow field. This contribution to the force and torque results from the distortion by the underlying strain rate of the vortical velocity disturbance
denotes the strain-rate tensor associated with the undisturbed flow field. This contribution to the force and torque results from the distortion by the underlying strain rate of the vortical velocity disturbance 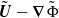 generated either by the dynamic boundary condition at the body surface
generated either by the dynamic boundary condition at the body surface 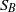 (and possibly on the wall
(and possibly on the wall 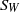 ), or/and by the vorticity
), or/and by the vorticity 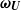 of the undisturbed flow within the core of the fluid. This extra term gives in turn rise to an additional contribution
of the undisturbed flow within the core of the fluid. This extra term gives in turn rise to an additional contribution 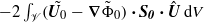 on the right-hand side of (3.13)–(3.15). This term was not present in the inviscid expressions established by Miloh (
on the right-hand side of (3.13)–(3.15). This term was not present in the inviscid expressions established by Miloh (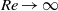 considered in the example of § 4.3, the disturbance is still irrotational outside the boundary layers that develop around the bubble and along the wall, respectively. The leading order in the vortical velocity disturbance is of
considered in the example of § 4.3, the disturbance is still irrotational outside the boundary layers that develop around the bubble and along the wall, respectively. The leading order in the vortical velocity disturbance is of 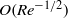 around the bubble, both in the
around the bubble, both in the 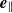 and
and 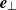 directions. Near the wall, it is of
directions. Near the wall, it is of 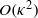 (respectively
(respectively 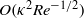 ) in the
) in the 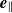 (respectively
(respectively 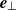 ) direction. Since the thickness of both boundary layers is of
) direction. Since the thickness of both boundary layers is of 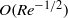 and
and 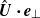 grows linearly with the distance to the wall, the extra term
grows linearly with the distance to the wall, the extra term 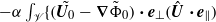
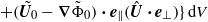 yields an
yields an 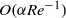 net contribution provided by the bubble boundary layer and only an
net contribution provided by the bubble boundary layer and only an 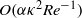 correction provided by the wall boundary layer. Hence the inviscid predictions (4.26) and (4.33) are unchanged and there is an
correction provided by the wall boundary layer. Hence the inviscid predictions (4.26) and (4.33) are unchanged and there is an 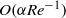 correction to the viscous drag and lift, similar in magnitude to that resulting from the term
correction to the viscous drag and lift, similar in magnitude to that resulting from the term 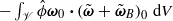 . Owing to the weak inhomogeneity assumption invoked in §§ 3.2 and 4.3, the dimensionless shear rate
. Owing to the weak inhomogeneity assumption invoked in §§ 3.2 and 4.3, the dimensionless shear rate  must be much smaller than unity for (4.26) and (4.33) to hold. Hence, in this context, the above corrections to the drag are much smaller than the leading,
must be much smaller than unity for (4.26) and (4.33) to hold. Hence, in this context, the above corrections to the drag are much smaller than the leading, 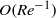 , contribution provided by the surface term
, contribution provided by the surface term 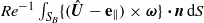 . Note that the above
. Note that the above 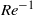 prefactor is missing on the right-hand side of (4.16) and (4.19).
prefactor is missing on the right-hand side of (4.16) and (4.19).