April 2024 Collection: Stochastic Calculus and Diffusions
Diffusion processes are continuous time Markov processes with (almost surely) continuous sample paths. They are defined in terms of stochastic differential equations, and the variety of tools available for solving and handling such equations are referred to as stochastic calculus, often applying celebrated theorems such as those of Itô and Girsanov.
Diffusions frequently appear as a limit of processes with discrete state spaces, and as approximations, they may be easier to handle than the original processes; this is, for example, the case in mathematical finance, where the dynamics in stock prices often are modelled by diffusions - with or without added jumps. Modern techniques in mathematical finance are almost entirely based on stochastic calculus.
Originating from physics more than a century ago, diffusion processes have become one of the most widespread mathematical objects used in stochastic modelling and applied probability, featuring applications in many areas such as insurance risk, queueing theory, biology and stochastic control, to mention a few.
Statistical techniques and the simulation of diffusions (and stochastic differential equations) are both intensive research areas overlapping with applied probability. In particular, Markov chain Monte Carlo and Exact simulation of diffusions and diffusion bridges are important when dealing with continuously or discretely observed diffusions.
Collection created by Professor Mogens Bladt (Københavns Universitet)
Original Article
A first-passage-place problem for integrated diffusion processes
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 55-67
-
- Article
-
- You have access
- HTML
- Export citation
Optimal discounted drawdowns in a diffusion approximation under proportional reinsurance
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 30 March 2022, pp. 527-540
-
- Article
- Export citation
Queues with path-dependent arrival processes
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 484-504
-
- Article
- Export citation
Weak convergence of stochastic integrals with respect to the state occupation measure of a Markov chain
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 23 June 2021, pp. 372-393
-
- Article
- Export citation
Exact simulation for multivariate Itô diffusions
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1003-1034
-
- Article
- Export citation
Research Papers
Analysis of a spatially inhomogeneous stochastic partial differential equation epidemic model
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 2 / 2020
- Published online by Cambridge University Press:
- 16 July 2020, pp. 613-636
-
- Article
- Export citation
Optimal stopping for the exponential of a Brownian bridge
- Part of:
-
- Journal:
- Journal of Applied Probability / Volume 57 / Issue 1 / 2020
- Published online by Cambridge University Press:
- 04 May 2020, pp. 361-384
-
- Article
- Export citation
General Applied Probability
The Λ-Fleming-Viot Process and a Connection with Wright-Fisher Diffusion
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1009-1035
-
- Article
-
- You have access
- Export citation
The Joint Laplace Transforms for Diffusion Occupation Times
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 4 / December 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1049-1067
-
- Article
-
- You have access
- Export citation
Occupation Times, Drawdowns, and Drawups for One-Dimensional Regular Diffusions
- Part of:
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 210-230
-
- Article
-
- You have access
- Export citation

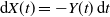
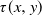
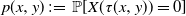
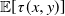
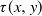
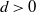
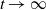
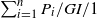
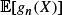 is analogous to the
is analogous to the