Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T06:08:54.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal discounted drawdowns in a diffusion approximation under proportional reinsurance

Part of: Stochastic systems and control Markov processes Stochastic processes

Published online by Cambridge University Press:  30 March 2022

Leonie Violetta Brinker Open the ORCID record for Leonie Violetta Brinker [Opens in a new window]  and
Hanspeter Schmidli Open the ORCID record for Hanspeter Schmidli [Opens in a new window]
Leonie Violetta Brinker*
Affiliation:
University of Cologne
Hanspeter Schmidli*
Affiliation:
University of Cologne
*
*Postal address: Department of Mathematics and Computer Science, University of Cologne, Weyertal 86–90, 50931 Cologne, Germany
*Postal address: Department of Mathematics and Computer Science, University of Cologne, Weyertal 86–90, 50931 Cologne, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

A diffusion approximation to a risk process under dynamic proportional reinsurance is considered. The goal is to minimise the discounted time in drawdown; that is, the time where the distance of the present surplus to the running maximum is larger than a given level 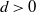$d > 0$ . We calculate the value function and determine the optimal reinsurance strategy. We conclude that the drawdown measure stabilises process paths but has a drawback as it also prevents surpassing the initial maximum. That is, the insurer is, under the optimal strategy, not interested in any more profits. We therefore suggest using optimisation criteria that do not avoid future profits.

Keywords

Drawdowndiffusion approximationoptimal proportional reinsuranceHamilton–Jacobi–Bellman equation

MSC classification

Secondary: 93E20: Optimal stochastic control 60G44: Martingales with continuous parameter 60J60: Diffusion processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 527 - 540
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albrecher, H. and Hipp, C. (2007). Lundberg’s risk process with tax. Blätter der DGVFM 28, 13–28.10.1007/s11857-007-0004-4CrossRefGoogle Scholar
Angoshtari, B., Bayraktar, E. and Young, V. R. (2015). Minimizing the expected lifetime spent in drawdown under proportional consumption. Finance Res. Lett. 15, 106–114.10.1016/j.frl.2015.08.010CrossRefGoogle Scholar
Angoshtari, B., Bayraktar, E. and Young, V. R. (2016). Optimal investment to minimize the probability of drawdown. Stochastics 88, 946–958.10.1080/17442508.2016.1155590CrossRefGoogle Scholar
Angoshtari, B., Bayraktar, E. and Young, V. R. (2016). Minimizing the probability of lifetime drawdown under constant consumption. Insurance Math. Econom. 69, 210–223.10.1016/j.insmatheco.2016.05.007CrossRefGoogle Scholar
Brinker, L. V. and Schmidli, H. (2020). Maximisation of dividends with a drawdown penalty in a diffusion approximation under proportional reinsurance. In preparation. University of Cologne.Google Scholar
Brinker, L. V. and Schmidli, H. (2021). Minimising the time in drawdown with an incentive to grow in a diffusion approximation under proportional reinsurance. In preparation. University of Cologne.Google Scholar
Chen, X., Landriault, D., Li, B. and Li, D. (2015). On minimizing drawdown risks of lifetime investments. Insurance Math. Econom. 65, 46–54.10.1016/j.insmatheco.2015.08.007CrossRefGoogle Scholar
Elworthy, K. D., Truman, A. and Zhao, H. (2007). Generalized Itô formulae and space-time Lebesgue–Stieltjes integrals of local times. In Séminaire de Probabilités XL, eds. C. Donati-Martin, M. Émery, A. Rouault and C. Stricker (Lecture Notes in Mathematics 1899). Springer, Berlin.CrossRefGoogle Scholar
Grandell, J. (1991). Aspects of Risk Theory. Springer, New York.10.1007/978-1-4613-9058-9CrossRefGoogle Scholar
Halidias, N. and Kloeden, P. E. (2006). A note on strong solutions of stochastic differential equations with a discontinuous drift coefficient. J. Appl. Math. Stoch. Anal. 2006, 1–6.10.1155/JAMSA/2006/73257CrossRefGoogle Scholar
Højgaard, B. and Taksar, M. (1998). Optimal proportional reinsurance policies for diffusion models. Scand. Actuarial J. 1998, 166–180.10.1080/03461238.1998.10414000CrossRefGoogle Scholar
Ikeda, N. and Watanabe, S. (1981). Stochastic Differential Equations and Diffusion Processes. North Holland, Amsterdam.Google Scholar
Lan, G. and Wu, J. (2014). New sufficient conditions of existence, moment estimations and non confluence for SDEs with non-Lipschitzian coefficients. Stochastic Process. Appl. 124, 4030–4049.10.1016/j.spa.2014.07.010CrossRefGoogle Scholar
Landriault, D., Li, B. and Zhang, H. (2017). On magnitude, asymptotics and duration of drawdowns for Lévy models. Bernoulli 23, 432–458.10.3150/15-BEJ748CrossRefGoogle Scholar
Mijatović, A. and Pistorius, M. R. (2012). On the drawdown of completely asymmetric Lévy processes. Stochastic Process. Appl. 122, 3812–3836.10.1016/j.spa.2012.06.012CrossRefGoogle Scholar
Pilipenko, A. (2014). An Introduction to Stochastic Differential Equations with Reflection. Potsdam University Press.Google Scholar
Schmidli, H. and Vierkötter, M. (2017). On optimal dividends with exponential and linear penalty payments. Insurance Math. Econom. 72, 265–270.Google Scholar
Schmidli, H. (2018). Risk Theory. Springer, Cham.Google Scholar
Yamada, T. (1973). On a comparison theorem for solutions of stochastic differential equations and its applications. J. Math. Kyoto Univ. 13, 497–512.Google Scholar
Zhang, H. (2015). Occupation times, drawdowns, and drawups for one-dimensional regular diffusions. Adv. Appl. Prob. 47, 210–230.10.1239/aap/1427814588CrossRefGoogle Scholar
Zhang, H., Leung, T. and Hadjiliadis, O. (2013). Stochastic modeling and fair valuation of drawdown insurance. Insurance Math. Econom. 53, 840–850.10.1016/j.insmatheco.2013.10.006CrossRefGoogle Scholar