A brief review is given of planetary theories from Leverrier to Newcomb to the age of computers. The presently used planetary theories are discussed and the process of replacing these theories with new ones is described. Some difficulties in preparing new planetary theories and the observational discrepancies which have been encountered previously are discussed.

In order to improve the determination of the mixed terms in classical theories, we show how these terms may be derived from a general theory developed with the same variables (of a keplerian nature). We find that the general theory of the first order in the masses already allows us to develop the mixed terms which appear at the second order in the classical theory. We also show that a part of the constant perturbation of the semi-major axis introduced in the classical theory is present in the general theory as very long-period terms; by developing these terms in powers of time, they would be equivalent to the appearance of very small secular terms (in t, t2, …) in the perturbation of the semi-major axes from the second order in the masses. The short period terms of the classical theory are found the same in the general theory, but without the numerical substitution of the values of the variables.

Mathematical construction of the general planetary theory has led to the series of two forms for the coordinates of eight major planets (excluding Pluto). The series of the first form are Poisson series where all orbital elements except the semi-major axes occur in literal shape. The series of the second form are polynomial-exponential series with respect to the time and serve to calculate the ephemerides. The arbitrary constants of the theory are related to the Keplerian elements. The terms of the zero and first degree in eccentricities and inclinations have been found in the second approximation with, respect to the disturbing masses. Among those of particular interest are the resonant terms caused by the commensurabilities of the mean notations of triplets of planets.

In this paper the method of determination of the planetary perturbations is proposed which is a modification of Dziobek-Brouwer’s method [1,2]. For the simplicity the case of two mutually disturbing planets is considered. In the original version of the method the perturbations of rectangular planetary coordinates are presented by means of the formal integrals

where index i corresponds to the number of the planet; δXik are perbations of Xik coordinates; Gik – components of the perturbating accelerations. The coefficients of aik, cik bij are the well-known functions of the coordinates of the elliptic motion which can be developed as double Fourier series in mean longitudes. The denominators in Davis’ formulas [3] for these coefficients contain the eccentricities. For this reason Musen [4] expressed an opinion that Brouwer’s method would lose its effectiveness when small eccentricities are involved. These fictitious peculiarities are eliminated in the present paper by means of trivial transformations and the expressions for the coefficients are given in a simple symmetric form.

The stability of the three-body problem formed by the Sun, Jupiter and Saturn is investigated using surfaces of zero velocity. The results obtained with the models of the restricted and general problems of three bodies are compared with numerical integration. The system is found to be stable in the sense that Saturn will neither interrupt the (perturbed) binary orbit of Jupiter around the Sun, nor will it escape from the system. It is shown that the known classical triple stellar systems are “more stable” than the solar system, which in turn is “more stable” than the Earth-Moon system.

The aim of this work is to study perturbations of planets of a period of some thousands of years. The use of an analytical method allows us to separate all different influences, e.g. near resonances and is combined with the very precise method of the numerical integration. The truncation to low orders can be avoided which is made by analytical methods in using developments with respect to the small parameters inclinations and eccentricities. For this purpose a special form of the Lagrange Equations is used where the terms containing the inverse distancefrom the planet to the perturbing one are separated as it is the most difficult to compute. To develop this a specific formulation has been found where the short periodic terms can precisely be determined. Although the development seems to be of a certain complexity the small numbers of quantities used can be tabulated once and for all in a specific problem. It should be possible to integrate the new form of the Lagrange Equations within a reasonable computer-time to determine the long periodic perturbations.

Les théories planétaires avec termes séculaires ne sont valables, par suite de la présence de termes augmentant avec le temps dans les éléments métriques, que dans un intervalle de temps limité (de l’ordre de mille ans) mais on peut les construire avec une bonne précision sur cet intervalle. Les recherches récentes sur la construction de formulaires pour le développement de la fonction perturbatrice bien adaptés au calcul sur ordinateur (Iszak 1964, Brumberg 1967, Chapront 1970) et les progrès réalisés dans les méthodes de calcul utilisées (Chapront et al. 1974) nous permettent d’espérer une amélioration sensible des théories existantes et des éphémérides qui en résultent.

La construction de théories planétaires précises est un travail long et, pour ce qui nous concerne, n’est pas encore achevée. Aussi, les résultats dont nous parlerons ici ne sont que des résultats provisoires. Nous développerons quelques aspects des difficultés que nous avons rencontrées et les conséquences de ces difficultés sur l’orientation des méthodes utilisées pour résoudre les problèmes suivant qu’il s’agit des planètes intérieures ou des grosses planètes.

The tidal theory of the evolution of the lunar orbit has remained inconsistent with the observational values of the apparent secular accelerations of the Sun and Moon since it was first developed by Jeffreys in 1920. Allowance for a changing moment of inertia of the Earth enables the discrepancy to be completely removed if a decrease is occurring at a rate of just about the amount already required by the phase-change theory of the nature of the terrestrial core. The agreement of the resulting theory with the latest determinations of the lunar acceleration increases confidence in the phase-change hypothesis. On the other hand the theory renders it most unlikely that a changing constant of gravitation will prove necessary to account for the observations. On the present theory of itself the Moon would have been extremely close to the Earth only about 109 years ago which suggests that some additional process may at times have influenced the lunar orbit.

Recently, M. W. Ovenden has raised seemingly plausible dynamical arguments which suggest that a 90-earth-mass planet existed in the present location of the asteroid belt until 16×106 years ago, and then rapidly disintegrated. He mentions supporting evidence from the cosmic ray exposure ages of chondritic meteorites. If the long-period comets originated from the recent disintegration of such a planet, several otherwise improbable characteristics of their orbits would be predicted, including a tendency for those orbits which are least perturbed to return to the site of the original break-up. In this investigation, we compare observed characteristics of long-period comet orbits with expected characteristics, based on the missing planet hypothesis. The conclusion is that long-period comet orbits are wholly consistent with the hypothesis; indeed, certain of their characteristics are difficult to explain in any other way.

Integrating backwards in time in the circular restricted three-body problem Galaxy-Sun-Comet, for both the real long-period comets and fictitious random sets of orbital elements, we have confirmed van Flandern’s conclusion that there is a statistically-significant clustering of the orbits of real long-period comets, in heliocentric direction, some 5×106 years ago. The clustering is also significant in heliocentric distance, and is more marked if it is assumed that the comets have gone round the Sun more than once since the epoch of maximum clustering. We suggest that the “event” discovered by van Flandern is not the explosive disruption of a planet formerly in the asteroid belt, but the latest in a series of minor catastrophies, such as the collisional break-up of a pair of large asteroids.

Via the facilities provided by PL/I, the operating system is extended to allow automatic manipulations of Poisson series in literal form.

L’étude des perturbations planétaires de la Lune soulève un problème fondamental provenant de la différence de caractère entre la théorie de la Lune et la théorie des planètes. Si, les deux théories sont des cas particuliers du problème de trois corps, la distinction entre elles résulte d’une analyse classique basée sur les résultats de l’observation et de plusieurs études théoriques.

The feasibility of applying the Lie transform method to the problem of the physical libration of the Moon is investigated. By a succession of canonical transformations, the Hamiltonian of the problem is brought under a form suitable for perturbation technique. The mean value of the inclination of the angular momentum upon the ecliptic and the frequencies of the free libration are computed.

The short-period terms are removed by averaging from special equations of motion for commensurability cases of the three-dimensional, elliptic, restricted three-body problem. Some examples of retrograde motion corresponding to the -1/1 commensurability, and an application to Hilda-type motion demonstrate the possibilities given by the method.

The paper constructs a long-periodic solution for the case of 1:1 resonance in the restricted problem of three bodies. The polar coordinates r and 0 appear in the form

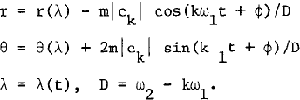
Here λ is the mean synodic longitude, m is the small mass-parameter, k is the integer nearest to the ratio ω2/ω1 of the fundamental angular frequencies of the motion, and ck is a Fourier coefficient of a certain periodic function. Only elementary functions enter r(λ) and θ(λ), while the calculation of λ(t) requires the inversion of a hyper-elliptic integral t(λ).

The internal resonant terms, carrying the critical divisor D, impart to the orbit an epicyclic character, in qualitative accord with the results of the numerical integration by Deprit and Henrard (1970). Our solution is valid except in the vicinity of the singularities at D = 0 and λ = 0.

The presence of the resonant terms invalidates the Brown conjecture (1911) regarding the termination of the family of the tadpoleshaped orbits at the Lagrangian point L3. However, this conjecture holds for the mean orbits defined by r = r(λ), θ = θ(λ), and it also holds in the limit as m → 0.

A generalized Hamiltonian formalism is established which is invariant not only under canonical transformations but under arbitrary transformations. Moreover the dependent variables, coordinates and momenta, as well as the independent variable are allowed to be transformed. This is to say that instead of the physical time t another independent variable s is used, such that t becomes a dependent variable or, more precisely, an additional coordinate. The formalism under consideration permits also to include nonconservative forces.

In case of Keplerian motion we propose to use the eccentric anomaly as the independent variable. By virtue of our generalized point of view a Lyapunov-stable differential system is obtained, such that all coordinates, including the time t, are computed by stable procedures. This stabilization is performed by control terms. As a new result a stabilizing control term also for the time integration is established, such that no longer any kind of time element is needed. This holds true for the usual coordinates as well as for the KS-coordinates.

Runge-Kutta methods of order p that utilize in derivatives of the equations of motion are presented. The results of applying these methods are compared to other special perturbation techniques for several test problems.