No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
The paper constructs a long-periodic solution for the case of 1:1 resonance in the restricted problem of three bodies. The polar coordinates r and 0 appear in the form
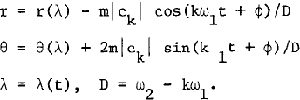
Here λ is the mean synodic longitude, m is the small mass-parameter, k is the integer nearest to the ratio ω2/ω1 of the fundamental angular frequencies of the motion, and ck is a Fourier coefficient of a certain periodic function. Only elementary functions enter r(λ) and θ(λ), while the calculation of λ(t) requires the inversion of a hyper-elliptic integral t(λ).
The internal resonant terms, carrying the critical divisor D, impart to the orbit an epicyclic character, in qualitative accord with the results of the numerical integration by Deprit and Henrard (1970). Our solution is valid except in the vicinity of the singularities at D = 0 and λ = 0.
The presence of the resonant terms invalidates the Brown conjecture (1911) regarding the termination of the family of the tadpoleshaped orbits at the Lagrangian point L3. However, this conjecture holds for the mean orbits defined by r = r(λ), θ = θ(λ), and it also holds in the limit as m → 0.