The variety O2 of all algebras (L; ∧, ∨, f, g, 0, 1) of type (2, 2, 1, 1, 0, 0) such that (L; ∧, ∨, f, 0, 1) and (L; ∧, ∨, g, 0, 1) are Ockham algebras is introduced, and, for n, m εℕ, its subvarieties DMSn, of double MSn-algebras, and DKn,m, of double Kn,m-algebras, are considered. It is shown that DKn,m has equationally definable principal congruences: a description of principal congruences on double Kn,m-algebras is given and simplified for double MSn-algebras. A topological duality for O2-algebras is developed and used to determine the subdirectly irreducible algebras in DKn,m and in DMSn. Finally, MSn-algebras which are reduct of a (unique) double MSn-algebra are characterized.

In [9] J. L. Krivine and B. Maurey introduced the class of stable Banach spaces: a separable Banach space is called stable if for every pair of bounded sequences (xn)n, (yn)n and for every pair of ultrafilters on the natural numbers we have

Many special cases of the equation x2+C= yn where x and y are positive integers and n≥3 have been considered over the years, but most results for general n are of fairly recent origin. The earliest reference seems to be an assertion by Fermat that he had shown that when C=2, n=3, the only solutions are given by x = 5, y = 3; a proof was published by Euler [1]. The first result for general n is due to Lebesgue [2] who proved that when C = 1 there are no solutions. Nagell [4] generalised Fermat's result and proved that for C = 2 the equation has no solution other than x = 5, y = 3, n = 3. He also showed [5] that for C = 4 the equation has no solution except x = 2, y = 2, n = 3 and x = 11, y = 5, n = 3, and claims in [6] to have dealt with the case C = 5. The case C = -1 was solved by Chao Ko, and an account appears in [3], pp. 302–304.

Let R and S be arbitrary rings, RM and SN countably generated free modules, and let φ:End(RM)→End(sN) be an isomorphism between the endomorphism rings of M and N. Camillo [3] showed in 1984 that these assumptions imply that R and S are Morita equivalent rings. Indeed, as Bolla pointed out in [2], in this case the isomorphism φ must be induced by some Morita equivalence between R and S. The same holds true if one assumes that RM and SN are, more generally, non-finitely generated free modules.

The notation in this paper will be standard and it may be found in [3], for example. In particular, the notation A ⊂′ B stands for the statement “A is an essential submodule of B”. As is customary, we say that a ring R is a Goldie ring when R is both left and right Goldie. Similarly, a ring is noetherian if and only if it is both right and left noetherian, etc.

The asymptotic behaviour has been determined for several natural geometric or topological quantities related to (degrees of) compactness of bounded linear operators on Banach spaces; see for instance [24], [25] and [17]. This paper complements these results by studying the spectral properties of some quantities related to weak compactness.

A Banach space E is said to have Property (w) if every operator from E into E' is weakly compact. This property was introduced by E. and P. Saab in [9]. They observe that for Banach lattices, Property (w) is equivalent to Property (V*), which in turn is equivalent to the Banach lattice having a weakly sequentially complete dual. Thus the following question was raised in [9].

Does every Banach space with Property (w) have a weakly sequentially complete dual, or even Property (V*)?

In this paper, we give two examples, both of which answer the question in the negative. Both examples are James type spaces considered in [1]. They both possess properties stronger than Property (w). The first example has the property that every operator from the space into the dual is compact. In the second example, both the space and its dual have Property (w). In the last section we establish some partial results concerning the problem (also raised in [9]) of whether (w) passes from a Banach space E to C(K, E).

Let G be a finite group, (ZG) the group of units of the integral group ring ZG and 1(ZG) the subgroup of units of augmentation 1. In this paper, we are primarily concerned with the problem of describing constructively (ZG) for particular groups G. This has been done for a small number of groups (see [11] for an excellent survey), and most recently Jespers and Leal [3] described (ZG) for several 2-groups. While the situation is clear for all groups of order less than 16, not all groups of order 16 were discussed in their paper. Our main aim is to complete the description of (ZG) for all groups of order 16. Since the structure of the unit group of abelian groups is very well known (see for example [10]), we are only interested in the non-abelian case.

The concept of reduction and integral closure of ideals relative to Artinian modules were introduced in [7]; and we summarize some of the main aspects now.

Let A be a commutative ring (with non-zero identity) and let a, b be ideals of A. Suppose that M is an Artinian module over A. We say that a is a reduction of b relative to M if a ⊆ b and there is a positive integer s such that

)O:Mabs)=(O:Mbs+l).

An element x of A is said to be integrally dependent on a relative to M if there exists n y ℕ(where ℕ denotes the set of positive integers) such that

It is shown that this is the case if and only if a is a reduction of a+Ax relative to M; moreover

ᾱ={x ɛ A: xis integrally dependent on a relative to M}

is an ideal of A called the integral closure of a relative to M and is the unique maximal member of

℘ = {b: b is an ideal of A which has a as a reduction relative to M}.

For any group G, denote by φf(G respectively L(G)) the intersection of all maximal subgroups of finite index (respectively finite nonprime index) in G, with the usual provision that the subgroup concerned equals Gif no such maximals exist. The subgroup φf(G) was discussed in [1] in connection with a property v possessed by certain groups: a group G has v if and only if every nonnilpotent, normal subgroup of G has a finite, nonnilpotent G-image. It was shown there, for instance, that G/φf(G) has v for all groups G. The subgroup L(G), in the case where G is finite, was investigated at some length in [3], one of the main results being that L(G) is supersoluble. (A published proof of this result appears as Theorem 3 of [4]). The present paper is concerned with the role of L(G) in groups G having property v or a related property a, the definition of which is obtained by replacing “nonnilpotent” by “nonsupersoluble” in the definition of v. We also present a result (namely Theorem 4) which displays a close relationship between the subgroups L(G) and φf(G) in an arbitrary group G. Some of the results for finite groups in [3] are found to hold with rather weaker hypotheses and, in fact, remain true for groups with v or a. We recall that if a group has a it also has v ([2]Theorem 2) but not conversely. For example, G = (x, y: y-1xy = x2)has v but not a. It is a well-known result of Gaschütz ([8], 5.2.15) that, in a finite group G, if His a normal subgroup containing φ(G) such that H/φ(G) is nilpotent than His nilpotent. This remains true in the case where G is any group with v [1, Proposition 1]. Our first result is in a similar vein and is a generalization of Theorem 9 of [7] and Theorem 1.2.9 of [3], the latter of which states that, for a finite group G, if G/L(G) is supersoluble, then so is G.

If A and B are torsion-free groups, and W is a cyclically reduced word of even length in A*B, it is generally conjectured that a Freiheitssatz holds, namely that each of A and B are embedded via the natural map into the one-relator product group G = (A*B)/N(W), where N denotes normal closure. If W has length 2, then G is a free product of A and B with infinite cyclic amalgamation, and the result is obvious. The purpose of this note is to prove the Freiheitssatz in some special cases.

In this paper we prove an identity between sums of reciprocals of Fibonacci and Lucas numbers. The Fibonacci numbers are defined for all n ≥ 0 by the recurrence relation Fn + 1 = Fn + Fn-1 for n ≥ 1, where F0 = 0 and F1 = 0. The Lucas numbers Ln are defined for all n ≥ 0 by the same recurrence relation, where L0 = 2 and L1 = 1 We prove the following identify.

Let G be a finite abelian group of rank m, M an oriented compact connected surface, and F(G, M) the set of all orientation preserving free G-actions on M. Two actions φ1, φ2εF(G, M) are equivalent if there exists an orientation preserving homeomorphism h of M such that

hφ1(f) for all f ε G.

We establish a necessary and sufficient condition for the existence of a positive solution of the integrodifferential equation

where nis an increasing real-valued function on the interval [0, α); that is, if and only if the characteristic equation

admits a positive root.

Consider the difference equation , where is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].

Recently, there has been some interest in the existence or the non-existence of positive solutions or the oscillation behavior of some difference equations. See Ladas, Philos and Sficas [6], [7].

The purpose of this paper is to investigate the positive solutions of integrodifferential equations (Section 1) and difference equations (Section 2) with unbounded delay. We obtain also some results for integrodifferential and difference inequalities.

An algebra L = L = (A; V, Λ, *, +, 0, 1) of type (2, 2, 1, 1, 0, 0) is called a distributive double p-algebra whenever its reduct (A, V, Λ, 0, 1) is a distributive (0, 1)-lattice that, for any a ∈ A, contains a greatest element a* such that a Λ a* = 0 and a least element a+ for which a v a+ = 1.

Let E be a Hausdorff locally convex space with continuous dual E1 and let M be a subspace of the algebraic dual E* such that M ∩ E1 = {0} and dim M = ℵ0. In the terminology of [4] the Mackey topology τ(E, E1 + M) is called a countable enlargement of τ(E, E1). There has been some interest in the question of when barrelledness is preserved under countable enlargements (see [4], [5], [6], [8], [9]). In this note we are concerned with the preservation of the quasidistinguished property for normed spaces under countable enlargements; this was posed as on open question by B. Tsirulnikov in [7]. According to [7] a Hausdorff locally convex space E is quasidistinguished if every bounded subset of its completion Ê is contained in the completion of a bounded subset of Ê (equivalently, in the closure in Ê of a bounded subset of E). Any normed space is clearly quasidistinguished and remains so under a finite enlargement (dim M < χ0) since the enlarged topology is normable. (See the Main Theorem of [7] for a general result on the preservation of the quasidistinguished property under finite enlargements.) We shall write QDCE for a countable enlargement which preserves the quasidistinguished property.

Normal-convex embeddings are introduced for inverse semigroups, generalizing the group-theoretic concept, due to Papakyriakopoulos [4]. It is shown that every E-unitary inverse semigroup admits a normal-convex embedding into a semidirect product of a semilattice by a group, a stronger version of a result by O'Carroll [3]. A general embedding result for inverse semigroups is also obtained.

Let F be a Banach space, (ω, ℱ, P) a fixed probability space, D a directed set filtering to the right with the order ≤, and (ℱt, D) a stochastic basis of ℱ, i.e. (ℱt, D) is an increasing family of sub-σ-algebras of ℱ:ℱs ⊂ for any s,t ε D and s≤t. Throughout this paper, (Xt) is an F-valued, (ℱt)-adapted sequence, i.e. Xt, is ℱt-measurable, t ε D. We also assume that Xt, ∈ L1, i.e. ∫ ∥Xt∥ <∞. We use I(H) to denote the indicator function of an event H. Let ∞ be a such element: t <∞, t ∈ D, 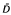= D ∪ ∞, and ℱ∞ = σ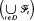. A stopping time is a map τ:Ω→ 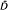such that (τ<t) ∈ ℱt, t ∈ D. A stopping time τ is called simple (countable) if it takes finitely (countably) many values in D(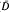). Let T and Tc be the sets of simple and countable stopping times respectively and Tf = {τ ∈ Tc: τ<∞ a.s.}. Clearly, (T, <) and (Tf, <) are directed sets filtering to the right. For τ ∈ Tc, let

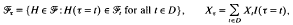
and

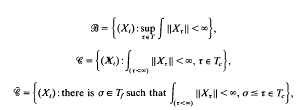
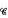= {(Xt): there is σ∈ Tf such that ∫(ι<∞) ∥Xι∥ < ∞, σ ≤ τ ∈ Tc},

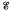= {(Xt):(Xι, ι ∈ T) converges stochastically (i.e. in probability) in the norm topology},

ℰ = {(Xt):(Xι, ι ∈ T) converges essentially in the norm topology}.

Let {a, b} designate the Pythagorean ratio (a2 - b2)/2ab between the sides of a rational right angled triangle. This paper studies the circumstances in which Pythagorean ratios can occupy consecutive places in an arithmetic progression. Part I deals with sets of three such ratios, while Part II discusses sets of four ratios.

In [6] B. H. Neumann proved the following beautiful result: if a group G is covered by finitely many cosets, say G = xiHi, then we can omit from the union any xiHi, for which |G|Hj| is infinite. In particular, |G:Hj| is finite, for some j ∈ {l,…,n}.

In an unpublished result R. Baer characterized the groups covered by finitely many abelian subgroups, they are exactly the centre-by-finite groups [8]. Coverings by nilpotent subgroups or by Engel subgroups and by normal subgroups have been studied, for example, by R. Baer (see [8]), L. C. Kappe [2,1], M. A. Brodie and R. F. Chamberlain [1], and recently by M. J. Tomkinson [9].