Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T07:36:29.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Units of group rings of groups of order 16

Published online by Cambridge University Press:  18 May 2009

E. Jespers  and
M. M. Parmenter
E. Jespers
Affiliation:
Department of Mathematics and StatisticsMemorial University of Newfoundland St. John's, NewfoundlandCanadaA1C 5S7
M. M. Parmenter
Affiliation:
Department of Mathematics and StatisticsMemorial University of Newfoundland St. John's, NewfoundlandCanadaA1C 5S7
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

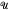Let G be a finite group, (ZG) the group of units of the integral group ring ZG and 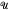1(ZG) the subgroup of units of augmentation 1. In this paper, we are primarily concerned with the problem of describing constructively 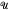(ZG) for particular groups G. This has been done for a small number of groups (see [11] for an excellent survey), and most recently Jespers and Leal [3] described 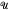(ZG) for several 2-groups. While the situation is clear for all groups of order less than 16, not all groups of order 16 were discussed in their paper. Our main aim is to complete the description of 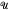(ZG) for all groups of order 16. Since the structure of the unit group of abelian groups is very well known (see for example [10]), we are only interested in the non-abelian case.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 3 , September 1993 , pp. 367 - 379
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Bass, H., The Dirichlet unit theorem, induced characters and Whitehead groups of finite groups, Topology 4 (1966), 391–410.CrossRefGoogle Scholar
2.Cliff, G. H., Sehgal, S.K. and Weiss, A. R., Units of integral group rings of metabelian groups, J. Algebra 73 (1981), 167–185.CrossRefGoogle Scholar
3.Jespers, E. and Leal, G., Describing units of integral group rings of some 2-groups, Comm. Algebra 19 (1991), 1809–1827.CrossRefGoogle Scholar
4.Jespers, E., Leal, G. and Parmenter, M. M., Bicyclic and Bass cyclic units in group rings, Canad. Math. Bull. to appear.Google Scholar
5.Newman, M., Integral matrices (Academic Press, 1972).Google Scholar
6.Parmenter, M. M., Torsion-free normal complements in unit groups of integral group rings, C.R. Math. Rep. Acad. Sci. Canada 12 (1990), 113–118.Google Scholar
7.Pollard, H. and Diamond, H. G., The theory of algebraic numbers, The Carus Mathematical Monographs (Mathematical Association of America, 1975).CrossRefGoogle Scholar
8.Ritter, J. and Sehgal, S. K., Generators of subgroups of U(ZG), Representation theory, group rings, and coding theory, Contemp. Math. 93 (Amer. Math. Soc., 1989), 331–347.CrossRefGoogle Scholar
9.Ritter, J. and Sehgal, S. K., Construction of units in integral group rings of finite nilpotent groups, Trans. Amer. Math. Soc. 324 (1991), 603–621.CrossRefGoogle Scholar
10.Sehgal, S. K., Topics in group rings (Marcel Dekker, 1978).Google Scholar
11.Sehgal, S. K., Units of integral group rings–A survey, preprint.Google Scholar