Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T19:58:14.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering a group with isolators of finitely many subgroups

Published online by Cambridge University Press:  18 May 2009

Patrizia Longobardi ,
Mercede Maj  and
Akbar H. Rhemtulla
Patrizia Longobardi
Affiliation:
Dlpartimento di Matematica e ApplicazioniUniversita degli Studi di Napolivia Cinthia, Monte S. Angelo80126 Naples– Italy
Mercede Maj
Affiliation:
Dlpartimento di Matematica e ApplicazioniUniversita degli Studi di Napolivia Cinthia, Monte S. Angelo80126 Naples– Italy
Akbar H. Rhemtulla
Affiliation:
Dept. of MathematicsUniversity of AlbertaEdmonton, AlbertaCanada T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [6] B. H. Neumann proved the following beautiful result: if a group G is covered by finitely many cosets, say G = 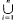xiHi, then we can omit from the union any xiHi, for which |G|Hj| is infinite. In particular, |G:Hj| is finite, for some j ∈ {l,…,n}.

In an unpublished result R. Baer characterized the groups covered by finitely many abelian subgroups, they are exactly the centre-by-finite groups [8]. Coverings by nilpotent subgroups or by Engel subgroups and by normal subgroups have been studied, for example, by R. Baer (see [8]), L. C. Kappe [2,1], M. A. Brodie and R. F. Chamberlain [1], and recently by M. J. Tomkinson [9].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 253 - 259
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Brodie, M. A., Chamberlain, R. F. and Kappe, L.-C., Finite coverings by normal subgroups, Proc. Amer. Math. Soc., 104 no. 3 (1988), 669–674.CrossRefGoogle Scholar
2.Kappe, L.-C., Finite coverings by 2-Engel groups, Bull. Austral. Math. Soc., 38 (1988), 141–150.CrossRefGoogle Scholar
3.Kirkinskii, A. S., Intersection of finitely generated subgroups in metabelian groups, Algebra and Logic, 20 no. 1 (1981), 22–36 (Algebra i Logika, 37–54).CrossRefGoogle Scholar
4.Lennox, J. C., Bigenetic properties of finitely generated hyper-(abelian-by-finite) groups, J. Austral. Math. Soc., 16 (1973), 309–315.CrossRefGoogle Scholar
5.Lennox, J. C. and Wiegold, J., Extension of a problem of Paul Erdös on groups, J. Austral. Math. Soc., Ser. A, 31 (1981), 459–463.CrossRefGoogle Scholar
6.Neumann, B. H., Groups covered by permutable subsets, J. London Math. Soc, 29 (1954), 236–248.CrossRefGoogle Scholar
7.Rhemtulla, A. H. and Wehrfritz, B. A. F., Isolators in soluble groups of finite rank, Rocky Mountain J. Math., 14 no. 2 (1984), 415–421.CrossRefGoogle Scholar
8.Robinson, D. J. S., Finiteness conditions and generalized soluble groups, vol. I, II, Springer-Verlag, Berlin–New York, 1972.CrossRefGoogle Scholar
9.Tomkinson, M. J., Hypercentre-by-finite groups, Publ. Math. Debrecen 40 (1992), 313–321.CrossRefGoogle Scholar