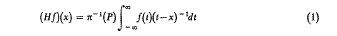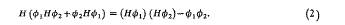Research Article
Twisted group rings which are semi-prime Goldie rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-11
-
- Article
-
- You have access
- Export citation
Inverse semigroups as extensions of semilattices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 12-21
-
- Article
-
- You have access
- Export citation
Group structure and properties of block ideals of the group algebra
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 22-28
-
- Article
-
- You have access
- Export citation
A simple ring separating certain radicals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 29-31
-
- Article
-
- You have access
- Export citation
Commutative rings whose quotients are Goldie
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 32-33
-
- Article
-
- You have access
- Export citation
Some generating-function equivalences†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 34-39
-
- Article
-
- You have access
- Export citation
Proper Dubreil-Jacotin inverse semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 40-51
-
- Article
-
- You have access
- Export citation
On Tricomi's relation for the Hilbert transformation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 52-56
-
- Article
-
- You have access
- Export citation
Abelian ergodic theorems for vector-valued functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-60
-
- Article
-
- You have access
- Export citation
On the role of L-Baire functions in abstract measure and integration
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 61-67
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 16 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation