Research Article
Prime and semiprime semigroup rings of cancellative semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-12
-
- Article
-
- You have access
- Export citation
On ternary quadratic forms that represent zero
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 13-23
-
- Article
-
- You have access
- Export citation
Bifree objects in e-varieties of strict orthodox semigroups and the lattice of strict orthodox *-semigroup varieties
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 25-37
-
- Article
-
- You have access
- Export citation
The congruence lattice of an ideal extension of semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-50
-
- Article
-
- You have access
- Export citation
Pairs of quadratic forms modulo one
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 51-61
-
- Article
-
- You have access
- Export citation
A note on the characterisation of eigencurves for certain two parameter eigenvalue problems in ordinary differential equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-67
-
- Article
-
- You have access
- Export citation
Tilting modules and a theorem of Hoshino
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 69-77
-
- Article
-
- You have access
- Export citation
Weakly stable Banach spaces and the Banach-Saks properties
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 79-83
-
- Article
-
- You have access
- Export citation
A spectral radius problem connected with weak compactness
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 85-94
-
- Article
-
- You have access
- Export citation
On Frattini-like subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 95-98
-
- Article
-
- You have access
- Export citation
One-relator products of torsion-free groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-104
-
- Article
-
- You have access
- Export citation
Positive solutions of integrodifferential and difference equations with unbounded delay
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 105-113
-
- Article
-
- You have access
- Export citation
Normal-convex embeddings of inverse semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 115-121
-
- Article
-
- You have access
- Export citation
Cohomological periodicity in graph products of combinatorially aspherical groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-129
-
- Article
-
- You have access
- Export citation
Invariant ideals of commutative rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-134
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 35 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 35 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

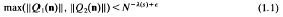
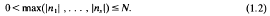
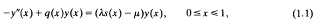

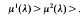
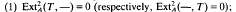
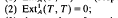
 on the natural numbers we have
on the natural numbers we have
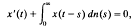
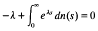
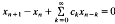 , where
, where 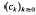 is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation
is a sequence of non-negative numbers. We prove this has positive solution if and only if the characteristic equation 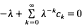 admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].
admits a root in (0, 1). For general results on integrodifferential equations we refer to the book by Burton [1] and the survey article by Corduneanu and Lakshmikantham [2]. Existence of a positive solution and oscillations in integrodifferential equations or in systems of integrodifferential equations recently have been investigated by Ladas, Philos and Sficas [5], Györi and Ladas [4], Philos and Sficas [12], Philos [9], [10], [11].