Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T14:41:21.572Z Has data issue: false hasContentIssue false
  • English
  • Français

Tilting modules and a theorem of Hoshino

Published online by Cambridge University Press:  18 May 2009

Ibrahim Assem  and
Otto Kerner
Ibrahim Assem
Affiliation:
Ibrahim Assem Mathématiques Et InformatiqueUniversité De SherbrookeSherbrooke, Quebec Canada, J1K 2R1
Otto Kerner
Affiliation:
Otto Kerner Mathematisches InstitutHeinrich Heine UniversitätUniversitätstr. 1 D-4000 Düsseldorf 1 Federal Republic of Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be an algebraically closed field, and A a finite dimensional k-algebra, which we shall assume, without loss of generality, to be basic and connected. By module is meant throughout a finitely generated right A-module. Following Happel and Ringel [10], we shall say that a module Tλ is a tilting (respectively, cotilting) module if it satisfies the following three conditions:

(1)

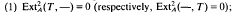
(2)

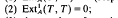
(3) the number of non-isomorphic indecomposable summands of T equals the rank of the Grothendieck group K0(A) of A.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 1 , January 1993 , pp. 69 - 77
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Assem, I., Torsion theories induced by tilting modules, Canad. J. Math. 36 (1984), 899–913.CrossRefGoogle Scholar
2.Assem, I., Tilting theory—an introduction. Topics in algebra, Rings and representations of algebras, Banach Center Publ. 26 part 1 (PWN, 1990), 127–180.Google Scholar
3.Assem, I. and Skowronski, A., Algebras with cycle-finite derived categories, Math. Ann. 280 (1988), 441–463.CrossRefGoogle Scholar
4.Assem, I. and Skowronski, A., Quadratic forms and iterated tilted algebras, J. Algebra 128 (1990), 55–85.CrossRefGoogle Scholar
5.Auslander, M. and Reiten, I., Representation theory of Artin algebras. III. Almost split sequences, and IV. Invariants given by almost split sequences, Comm. Algebra 3 (1975), 239–294, and 5 (1977), 443–518.CrossRefGoogle Scholar
6.Baer, D., A note on wild quiver algebras and tilting modules, Comm. Algebra 17 (1989), 751–757.CrossRefGoogle Scholar
7.Bongartz, K., Tilted algebras, Representations of algebras (Puebla, 1980), Lecture Notes in Math. 903 (Springer, 1981), 26–38.CrossRefGoogle Scholar
8.Bongartz, K. and Gabriel, P., Covering spaces in representation-theory, Invent. Math. 65 (1981/1982), 331–378.CrossRefGoogle Scholar
9.Happel, D., Triangulated categories in the representation theory of finite-dimensional algebras, London Mathematical Society Lecture Note Series 119 (Cambridge University Press, 1988).CrossRefGoogle Scholar
10.Happel, D. and Ringel, C. M., Tilted algebras, Trans. Amer. Math. Soc. 274 (1982), 399–443.CrossRefGoogle Scholar
11.Happel, D. and Ringel, C. M., Construction of tilted algebras, Representations of algebras (Puebla, 1980), Lecture Notes in Math. 903 (Springer, 1981), 125–144.CrossRefGoogle Scholar
12.Hoshino, M., Tilting modules and torsion theories, Bull. London Math. Soc. 14 (1982), 334–336.CrossRefGoogle Scholar
13.Hoshino, M., Modules without self-extensions and Nakayama's conjecture, Arch. Math. (Basel) 43 (1984), 493–500.CrossRefGoogle Scholar
14.Kerner, O., Tilting wild algebras, J. London Math. Soc. (2) 39 (1989), 29–47.CrossRefGoogle Scholar
15.Ringel, C. M., Tame algebras and integral quadratic forms, Lecture Notes in Math. 1099 (Springer, 1984).CrossRefGoogle Scholar
16.Ringel, C. M., The regular components of the Auslander-Reiten quiver of a tilted algebra, Chinese Ann. Math. Ser. B 9 (1988), 1–18.Google Scholar
17.Skowronski, A., Algebras of polynomial growth, Topics in algebra, Rings and representations of algebras, Banach Center Publ. 26 part 1 (PWN, 1990), 535–568.Google Scholar
18.SmalØ, S. O., Torsion theories and tilting modules, Bull. London Math. Soc. 16 (1984), 518–522.CrossRefGoogle Scholar