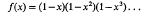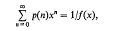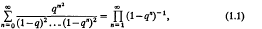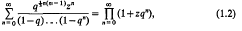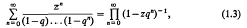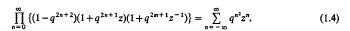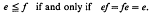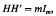Research Article
Matrix representations of semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
Proof of a conjecture of Ramanujan
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-32
-
- Article
-
- You have access
- Export citation
Enumerative proofs of certain q-identities
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-40
-
- Article
-
- You have access
- Export citation
Compact linear operators from an algebraic standpoint
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 41-49
-
- Article
-
- You have access
- Export citation
Some integral equations involving finite parts of divergent integrals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 50-54
-
- Article
-
- You have access
- Export citation
Naturally ordered bands
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-58
-
- Article
-
- You have access
- Export citation
A new class of Hadamard matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-62
-
- Article
-
- You have access
- Export citation
Automorphisms of the semigroup of all differentiable functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-66
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 8 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 8 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation