Research Article
Non-periodic bifurcations of one-dimensional maps
-
- Published online by Cambridge University Press:
- 09 January 2007, pp. 459-492
-
- Article
- Export citation
The structure of tame minimal dynamical systems
-
- Published online by Cambridge University Press:
- 01 December 2007, pp. 1819-1837
-
- Article
- Export citation
Gibbs properties of self-conformal measures and the multifractal formalism
-
- Published online by Cambridge University Press:
- 20 April 2007, pp. 787-812
-
- Article
- Export citation
Statistical properties of a skew product with a curve of neutral points
-
- Published online by Cambridge University Press:
- 28 November 2006, pp. 123-151
-
- Article
- Export citation
A new class of rank-one transformations with singular spectrum
-
- Published online by Cambridge University Press:
- 01 October 2007, pp. 1541-1555
-
- Article
- Export citation
A relative version of Connes' $\chi(M)$ invariant and existence of orbit inequivalent actions
-
- Published online by Cambridge University Press:
- 03 May 2007, pp. 1199-1213
-
- Article
- Export citation
Adapted metrics for dominated splittings
-
- Published online by Cambridge University Press:
- 01 December 2007, pp. 1839-1849
-
- Article
- Export citation
On the structure of strange non-chaotic attractors in pinched skew products
-
- Published online by Cambridge University Press:
- 20 December 2006, pp. 493-510
-
- Article
- Export citation
Weighted ergodic theorems and strong laws of large numbers
-
- Published online by Cambridge University Press:
- 12 February 2007, pp. 511-543
-
- Article
- Export citation
Fixed points of abelian actions on S2
-
- Published online by Cambridge University Press:
- 01 October 2007, pp. 1557-1581
-
- Article
- Export citation
On the structure of abstract Hubbard trees and the space of abstract kneading sequences of degree two
-
- Published online by Cambridge University Press:
- 11 June 2007, pp. 1215-1238
-
- Article
- Export citation
On the ergodicity of Weyl sum cocycles
-
- Published online by Cambridge University Press:
- 01 December 2007, pp. 1851-1863
-
- Article
- Export citation
Bounded orbit injections and suspension equivalence for minimal $\mathbb{Z}^2$ actions
-
- Published online by Cambridge University Press:
- 28 November 2006, pp. 153-182
-
- Article
- Export citation
Actions of dense subgroups of compact groups and II$_{1}$-factors with the Haagerup property
-
- Published online by Cambridge University Press:
- 12 March 2007, pp. 813-826
-
- Article
- Export citation
Stability of periodic points in piecewise isometries of Euclidean spaces
-
- Published online by Cambridge University Press:
- 20 December 2006, pp. 183-197
-
- Article
- Export citation
The actions of ${\mathit{Out}(F_k)}$ on the boundary of Outer space and on the space of currents: minimal sets and equivariant incompatibility
-
- Published online by Cambridge University Press:
- 20 April 2007, pp. 827-847
-
- Article
- Export citation
Flattening functions on flowers
-
- Published online by Cambridge University Press:
- 01 December 2007, pp. 1865-1886
-
- Article
-
- You have access
- Export citation
Damage spreading and $\mu$-sensitivity on cellular automata
-
- Published online by Cambridge University Press:
- 09 January 2007, pp. 545-565
-
- Article
- Export citation
Invariant densities for generalized β-maps
-
- Published online by Cambridge University Press:
- 01 October 2007, pp. 1583-1598
-
- Article
- Export citation
Orbits on a nilmanifold under the action of a polynomial sequence of translations
-
- Published online by Cambridge University Press:
- 03 May 2007, pp. 1239-1252
-
- Article
- Export citation

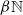 , or it is a ‘tame’ topological space whose topology is determined by the convergence of sequences. In the latter case, the dynamical system is said to be tame. We use the structure theory of minimal dynamical systems to show that, when the acting group is Abelian, a tame metric minimal dynamical system (i) is almost automorphic (i.e. it is an almost one-to-one extension of an equicontinuous system), and (ii) admits a unique invariant probability measure such that the corresponding measure-preserving system is measure-theoretically isomorphic to the Haar measure system on the maximal equicontinuous factor.
, or it is a ‘tame’ topological space whose topology is determined by the convergence of sequences. In the latter case, the dynamical system is said to be tame. We use the structure theory of minimal dynamical systems to show that, when the acting group is Abelian, a tame metric minimal dynamical system (i) is almost automorphic (i.e. it is an almost one-to-one extension of an equicontinuous system), and (ii) admits a unique invariant probability measure such that the corresponding measure-preserving system is measure-theoretically isomorphic to the Haar measure system on the maximal equicontinuous factor.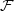 is a finitely generated abelian group of orientation preserving
is a finitely generated abelian group of orientation preserving 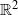 which leaves invariant a compact set then there is a common fixed point for all elements of
which leaves invariant a compact set then there is a common fixed point for all elements of 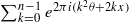 with
with 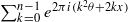 ,
, 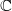 .
. . A pre-image selector is a map
. A pre-image selector is a map  with finitely many discontinuities, each of which is a jump discontinuity, and such that
with finitely many discontinuities, each of which is a jump discontinuity, and such that  . The closure of the image of a pre-image selector is called a flower and a flower with
. The closure of the image of a pre-image selector is called a flower and a flower with