Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Franks, John
and
Handel, Michael
2009.
Global fixed points for centralizers and Morita’s Theorem.
Geometry & Topology,
Vol. 13,
Issue. 1,
p.
87.
Feighn, Mark
and
Handel, Michael
2009.
Abelian subgroups of Out(Fn).
Geometry & Topology,
Vol. 13,
Issue. 3,
p.
1657.
Firmo, Saponga
2011.
Localisation des points fixes communs pour des difféomorphismes commutants du plan.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 42,
Issue. 3,
p.
373.
Mann, Kathryn
2012.
Bounded orbits and global fixed points for groups acting on the plane.
Algebraic & Geometric Topology,
Vol. 12,
Issue. 1,
p.
421.
Béguin, F.
Le Calvez, P.
Firmo, S.
and
Miernowski, T.
2013.
Des points fixes communs pour des difféomorphismes de qui commutent et préservent une mesure de probabilité.
Journal of the Institute of Mathematics of Jussieu,
Vol. 12,
Issue. 4,
p.
821.
Guelman, Nancy
and
Liousse, Isabelle
2013.
Actions of Baumslag-Solitar groups on surfaces.
Discrete & Continuous Dynamical Systems - A,
Vol. 33,
Issue. 5,
p.
1945.
Firmo, S.
Ribón, J.
and
Velasco, J.
2015.
Fixed points for nilpotent actions on the plane and the Cartwright–Littlewood theorem.
Mathematische Zeitschrift,
Vol. 279,
Issue. 3-4,
p.
849.
RIBÓN, JAVIER
2016.
Fixed points of nilpotent actions on.
Ergodic Theory and Dynamical Systems,
Vol. 36,
Issue. 1,
p.
173.
FIRMO, S.
and
RIBÓN, J.
2020.
Global fixed points for nilpotent actions on the torus.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 12,
p.
3339.


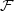 is a finitely generated abelian group of orientation preserving
is a finitely generated abelian group of orientation preserving 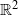 which leaves invariant a compact set then there is a common fixed point for all elements of
which leaves invariant a compact set then there is a common fixed point for all elements of 