ARTICLES
A BIAS-CORRECTED NONPARAMETRIC ENVELOPMENT ESTIMATOR OF FRONTIERS
-
- Published online by Cambridge University Press:
- 01 October 2009, pp. 1289-1318
-
- Article
- Export citation
TESTING FOR A UNIT ROOT IN THE PRESENCE OF A POSSIBLE BREAK IN TREND
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1545-1588
-
- Article
- Export citation
REPRESENTATION AND WEAK CONVERGENCE OF STOCHASTIC INTEGRALS WITH FRACTIONAL INTEGRATOR PROCESSES
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1589-1624
-
- Article
- Export citation
BOOTSTRAPPING SYSTEMS COINTEGRATION TESTS WITH A PRIOR ADJUSTMENT FOR DETERMINISTIC TERMS
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 243-269
-
- Article
- Export citation
Article Commentary
REJOINDER
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 658-667
-
- Article
- Export citation
ARTICLES
OPENING THE BLACK BOX: STRUCTURAL FACTOR MODELS WITH LARGE CROSS SECTIONS
-
- Published online by Cambridge University Press:
- 01 October 2009, pp. 1319-1347
-
- Article
- Export citation
DISCRETE TIME REPRESENTATIONS OF COINTEGRATED CONTINUOUS TIME MODELS WITH MIXED SAMPLE DATA
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1030-1049
-
- Article
- Export citation
Notes and Problems
QUASI-MAXIMUM LIKELIHOOD ESTIMATION OF SEMI-STRONG GARCH MODELS
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 561-570
-
- Article
- Export citation
ARTICLES
GMM ESTIMATION AND INFERENCE IN DYNAMIC PANEL DATA MODELS WITH PERSISTENT DATA
-
- Published online by Cambridge University Press:
- 01 October 2009, pp. 1348-1391
-
- Article
- Export citation
THE NEW ZEALAND BUSINESS CYCLE
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1050-1069
-
- Article
- Export citation
Research Article
VALIDITY OF SUBSAMPLING AND “PLUG-IN ASYMPTOTIC” INFERENCE FOR PARAMETERS DEFINED BY MOMENT INEQUALITIES
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 669-709
-
- Article
- Export citation
ARTICLES
ROBUST INFERENCE IN AUTOREGRESSIONS WITH MULTIPLE OUTLIERS
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1625-1661
-
- Article
- Export citation
LASSO-TYPE GMM ESTIMATOR
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 270-290
-
- Article
- Export citation
Notes and Problems
ALMOST SURE BOUNDS ON THE ESTIMATION ERROR FOR OLS ESTIMATORS WHEN THE REGRESSORS INCLUDE CERTAIN MFI(1) PROCESSES
-
- Published online by Cambridge University Press:
- 01 April 2009, pp. 571-582
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ECT volume 25 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 March 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
ASYMPTOTIC THEORY FOR LOCAL TIME DENSITY ESTIMATION AND NONPARAMETRIC COINTEGRATING REGRESSION
-
- Published online by Cambridge University Press:
- 01 June 2009, pp. 710-738
-
- Article
- Export citation
ARTICLES
THE LIMITS OF ECONOMETRICS: NONPARAMETRIC ESTIMATION IN HILBERT SPACES
-
- Published online by Cambridge University Press:
- 01 August 2009, pp. 1070-1086
-
- Article
- Export citation
THE PROPERTIES OF KULLBACK–LEIBLER DIVERGENCE FOR THE UNIT ROOT HYPOTHESIS
-
- Published online by Cambridge University Press:
- 01 December 2009, pp. 1662-1681
-
- Article
- Export citation
NOTES AND PROBLEMS
FINITE-SAMPLE MOMENTS OF THE COEFFICIENT OF VARIATION
-
- Published online by Cambridge University Press:
- 01 February 2009, pp. 291-297
-
- Article
- Export citation
ARTICLES
EFFICIENT SEMIPARAMETRIC SEEMINGLY UNRELATED QUANTILE REGRESSION ESTIMATION
-
- Published online by Cambridge University Press:
- 01 October 2009, pp. 1392-1414
-
- Article
- Export citation

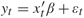 ,
, 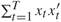 tends to infinity (a.s.) and log(
tends to infinity (a.s.) and log(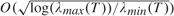 . In this note
. In this note