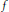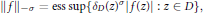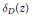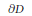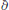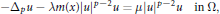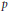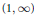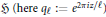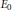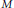Research Article
Weighted Brianchon-Gram Decomposition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-169
-
- Article
-
- You have access
- Export citation
On Sequences of Squares with Constant Second Differences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-491
-
- Article
-
- You have access
- Export citation
Polygons with Prescribed Gauss Map in Hadamard Spaces and Euclidean Buildings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 321-336
-
- Article
-
- You have access
- Export citation
On a Class of Singular Integral Operators With Rough Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
-
- Article
-
- You have access
- Export citation
Homotopy Equivalence and Groups of Measure-Preserving Homeomorphisms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 337-346
-
- Article
-
- You have access
- Export citation
Conjugacy Classes of Subalgebras of the Real Sedenions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 492-507
-
- Article
-
- You have access
- Export citation
The Geometry of d2y1/dt2 = f (y, ẏ, t) and d2y2/dt2 = g(y, ẏ, t), and Euclidean Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-184
-
- Article
-
- You have access
- Export citation
Going-Down Results for Ci-Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 11-20
-
- Article
-
- You have access
- Export citation
Evaluation of the Dedekind Eta Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 21-35
-
- Article
-
- You have access
- Export citation
Affine Completeness of Generalised Dihedral Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-357
-
- Article
-
- You have access
- Export citation
On the Inequality for Volume and Minkowskian Thickness
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 185-195
-
- Article
-
- You have access
- Export citation
Growth Spaces and Growth Norm Estimates for
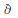 on Convex Domains of Finite Type
on Convex Domains of Finite Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 508-525
-
- Article
-
- You have access
- Export citation
Holomorphic Frames for Weakly Converging Holomorphic Vector Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 36-40
-
- Article
-
- You have access
- Export citation
On the Principal Eigencurve of the p-Laplacian: Stability Phenomena
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 358-370
-
- Article
-
- You have access
- Export citation
Another Proof of Totaro's Theorem on E8-Torsors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-202
-
- Article
-
- You have access
- Export citation
The Values of Modular Functions and Modular Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 526-535
-
- Article
-
- You have access
- Export citation
Inner E0-Semigroups on Infinite Factors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 371-380
-
- Article
-
- You have access
- Export citation
Measure Convex and Measure Extremal Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 536-548
-
- Article
-
- You have access
- Export citation
The Ganea and Whitehead Variants of the Lusternik–Schnirelmann Category
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 41-54
-
- Article
-
- You have access
- Export citation
The Ergodic Hilbert Transform for Admissible Processes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 203-212
-
- Article
-
- You have access
- Export citation

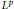
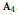

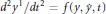
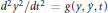
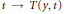
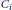
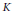
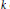
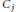
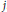

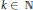


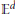
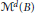
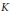
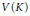
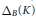
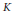
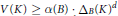
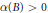
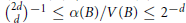
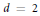
 on Convex Domains of Finite Type
on Convex Domains of Finite Type