No CrossRef data available.
Article contents
Going-Down Results for Ci-Fields
Published online by Cambridge University Press: 20 November 2018
Abstract
We search for theorems that, given a 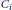 ${{C}_{i}}$-field
${{C}_{i}}$-field 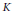 $K$ and a subfield
$K$ and a subfield 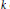 $k$ of
$k$ of 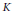 $K$, allow us to conclude that
$K$, allow us to conclude that 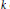 $k$ is a
$k$ is a 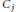 ${{C}_{j}}$ -field for some
${{C}_{j}}$ -field for some 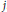 $j$. We give appropriate theorems in the case
$j$. We give appropriate theorems in the case 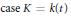 $\text{case }K=k\left( t \right)$ and
$\text{case }K=k\left( t \right)$ and 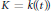 $K=k\left( \left( t \right) \right)$. We then consider the more difficult case where
$K=k\left( \left( t \right) \right)$. We then consider the more difficult case where 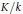 $K/k$ is an algebraic extension. Here we are able to prove some results, and make conjectures. We also point out the connection between these questions and Lang's conjecture on nonreal function fields over a real closed field.
$K/k$ is an algebraic extension. Here we are able to prove some results, and make conjectures. We also point out the connection between these questions and Lang's conjecture on nonreal function fields over a real closed field.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006


