Research Article
Generalisation de la Formule de Riemann-Hurwitz
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 761-767
-
- Article
-
- You have access
- Export citation
Ideals and Higher Derivations in Commutative Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-415
-
- Article
-
- You have access
- Export citation
On Inflation and Torsion of Amitsur Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 239-260
-
- Article
-
- You have access
- Export citation
Actions That Fiber and Vector Semigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-37
-
- Article
-
- You have access
- Export citation
Moore Spaces, Semi-Metric Spaces and Continuous Mappings Connected with Them
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1033-1042
-
- Article
-
- You have access
- Export citation
Normed Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 580-591
-
- Article
-
- You have access
- Export citation
Special (p;q) Radicals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-44
-
- Article
-
- You have access
- Export citation
Familles De Valuations A Caractere Compact
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 416-425
-
- Article
-
- You have access
- Export citation
Sums and Products of Normal Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 261-269
-
- Article
-
- You have access
- Export citation
Taming Wild Simple Closed Curves with Monotone Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 768-788
-
- Article
-
- You have access
- Export citation
Cyclic Maps From Suspensions to Suspensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 789-791
-
- Article
-
- You have access
- Export citation
Representation of Algebras with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 592-597
-
- Article
-
- You have access
- Export citation
Products of Locally Compact Groups with Zero and Their Actions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1043-1051
-
- Article
-
- You have access
- Export citation
A Functional Analytic Description of Normal Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 45-49
-
- Article
-
- You have access
- Export citation
A Generalization of “Concordance of PL-Homeomorphisms of Sp × Sq
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 426-431
-
- Article
-
- You have access
- Export citation
Extensions of One Primitive Inverse Semigroup by Another
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-278
-
- Article
-
- You have access
- Export citation
Multiplications on a Space with Finitely Many Non-Vanishing Homotopy Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1052-1062
-
- Article
-
- You have access
- Export citation
The Equality (A ∩ B)n = An ∩ Bn for Ideals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 792-798
-
- Article
-
- You have access
- Export citation
Condition that All Irreducible Representations of a Compact Lie Group, if Restricted to a Subgroup, Contain no Representation More than Once
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 432-438
-
- Article
-
- You have access
- Export citation
Extending Jordan Ideals and Jordan Homomorphisms of Symmetric Elements in a Ring with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-59
-
- Article
-
- You have access
- Export citation

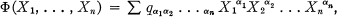
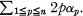
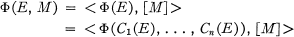
 acts on a space
acts on a space  , l'anneau de la valuation
, l'anneau de la valuation  , l'idéal maximal de l'anneau
, l'idéal maximal de l'anneau  l'anneau défini par la famille Ω; nous supposons toujours Ω tel que
l'anneau défini par la famille Ω; nous supposons toujours Ω tel que  et munissons Ω de la topologie la plus faible pour laquelle les
et munissons Ω de la topologie la plus faible pour laquelle les 