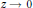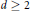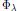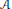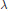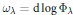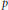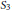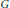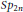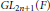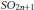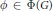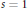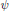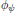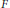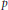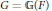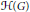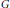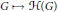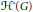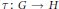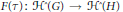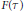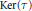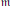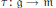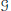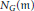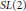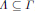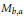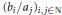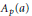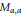We pr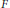ove a uniformcontrol as $z\,\to \,0$ for the resolvent ${{(P-z)}^{-1}}$ of long range perturbations $P$ of the Euclidean Laplacian in divergence form by combining positive commutator estimates and properties of Riesz transforms. These estimates hold in dimension $d\,\ge \,3$ when $P$ is defined on ${{\mathbb{R}}^{d}}$ and in dimension $d\,\ge \,2$ when $P$ is defined outside a compact obstacle with Dirichlet boundary conditions.

In this paper we study genus 2 curves whose Jacobians admit a polarized (4, 4)-isogeny to a product of elliptic curves. We consider base fields of characteristic different from 2 and 3, which we do not assume to be algebraically closed. We obtain a full classification of all principally polarized abelian surfaces that can arise from gluing two elliptic curves along their 4-torsion, and we derive the relation their absolute invariants satisfy.

As an intermediate step, we give a general description of Richelot isogenies between Jacobians of genus 2 curves, where previously only Richelot isogenies with kernels that are pointwise defined over the base field were considered.

Our main tool is a Galois theoretic characterization of genus 2 curves admitting multiple Richelot isogenies.

Every holomorphic function on a compact subset of a Riemann surface can be uniformly approximated by partial sums of a given series of functions. Those functions behave locally like the classical fundamental solutions of the Cauchy–Riemann operator in the plane.

If ${{\Phi }_{\lambda }}$ is a master function corresponding to a hyperplane arrangement $\mathcal{A}$ and a collection of weights $\lambda $, we investigate the relationship between the critical set of ${{\Phi }_{\lambda }}$, the variety defined by the vanishing of the one-form ${{\omega }_{\lambda }}=\text{d}\log {{\Phi }_{\lambda }}$, and the resonance of $\lambda $. For arrangements satisfying certain conditions, we show that if $\lambda $ is resonant in dimension $p$, then the critical set of ${{\Phi }_{\lambda }}$ has codimension at most $p$. These include all free arrangements and all rank 3 arrangements.

We analyze flat ${{S}_{3}}$-covers of schemes, attempting to create structures parallel to those found in the abelian and triple cover theories. We use an initial local analysis as a guide in finding a global description.

For a maximal torus in a quasi-split semi-simple simply-connected group over a local field of characteristic 0, Langlands and Shelstad constructed a cohomological invariant called the splitting invariant, which is an important component of their endoscopic transfer factors. We study this invariant in the case of a split real group and prove a decomposition theorem which expresses this invariant for a general torus as a product of the corresponding invariants for simple tori. We also show how this reduction formula allows for the comparison of splitting invariants between different tori in the given real group.

Let $G$ be the $F$-rational points of the symplectic group $S{{p}_{2n}}$, where $F$ is a non-Archimedean local field of characteristic 0. Cogdell, Kim, Piatetski-Shapiro, and Shahidi constructed local Langlands functorial lifting from irreducible generic representations of $G$ to irreducible representations of $G{{L}_{2n+1}}\left( F \right)$. Jiang and Soudry constructed the descent map from irreducible supercuspidal representations of $G{{L}_{2n+1}}\left( F \right)$ to those of $G$, showing that the local Langlands functorial lifting from the irreducible supercuspidal generic representations is surjective. In this paper, based on above results, using the same descent method of studying $S{{O}_{2n+1}}$ as Jiang and Soudry, we will show the rest of local Langlands functorial lifting is also surjective, and for any local Langlands parameter $\phi \,\in \,\Phi \left( G \right)$, we construct a representation $\sigma $ such that $\phi $ and $\sigma $ have the same twisted local factors. As one application, we prove the $G$-case of a conjecture of Gross-Prasad and Rallis, that is, a local Langlands parameter $\phi \,\in \,\Phi \left( G \right)$ is generic, i.e., the representation attached to $\phi $ is generic, if and only if the adjoint $L$-function of $\phi $ is holomorphic at $s\,=\,1$. As another application, we prove for each Arthur parameter $\psi $, and the corresponding local Langlands parameter ${{\phi }_{\psi }}$, the representation attached to ${{\phi }_{\psi }}$ is generic if and only if ${{\phi }_{\psi }}$ is tempered.

When $F$ is a 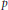$p$-adic field, and 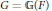$G\,=\,\mathbb{G}\left( F \right)$ is the group of 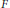$F$-rational points of a connected algebraic 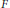$F$-group, the complex vector space 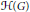$\mathcal{H}\left( G \right)$ of compactly supported locally constant distributions on 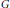$G$ has a natural convolution product that makes it into a $\mathbb{C}$-algebra (without an identity) called the Hecke algebra. The Hecke algebra is a partial analogue for 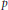$p$-adic groups of the enveloping algebra of a Lie group. However, 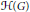$\mathcal{H}\left( G \right)$ has drawbacks such as the lack of an identity element, and the process 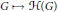$G\,\mapsto \,\mathcal{H}\left( G \right)$ is not a functor. Bernstein introduced an enlargement 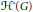${{\mathcal{H}}^{\hat{\ }}}\left( G \right)$ of 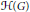$\mathcal{H}\left( G \right)$. The algebra 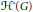${{\mathcal{H}}^{\hat{\ }}}\left( G \right)$ consists of the distributions that are left essentially compact. We show that the process 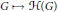$G\,\mapsto \,{{\mathcal{H}}^{\hat{\ }}}\left( G \right)$ is a functor. If 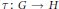$\tau \,:\,G\,\to \,H$ is a morphism of 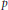$p$-adic groups, let 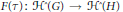$F\left( \tau \right):\,{{\mathcal{H}}^{\hat{\ }}}\left( G \right)\,\to \,{{\mathcal{H}}^{\hat{\ }}}\left( H \right)$ be the morphism of $\mathbb{C}$-algebras. We identify the kernel of 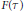$F\left( \tau \right)$ in terms of 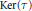$\text{Ker}\left( \tau \right)$. In the setting of $p$-adic Lie algebras, with $\mathfrak{g}$ a reductive Lie algebra, 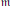$\mathfrak{m}$ a Levi, and 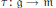$\tau \,:\,\mathfrak{g}\,\to \,\mathfrak{m}$ the natural projection, we show that 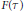$F\left( \tau \right)$ maps 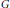$G$-invariant distributions on 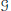$\mathcal{G}$ to 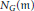${{N}_{G}}\left( \mathfrak{m} \right)$-invariant distributions on 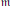$\mathfrak{m}$. Finally, we exhibit a natural family of 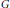$G$-invariant essentially compact distributions on $\mathfrak{g}$ associated with a 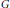$G$-invariant non-degenerate symmetric bilinear form on $\mathfrak{g}$ and in the case of 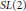$SL\left( 2 \right)$ show how certain members of the family can be moved to the group.

We inspect the relationship between relative Fourier multipliers on noncommutative Lebesgue–Orlicz spaces of a discrete group $\Gamma$ and relative Toeplitz-Schur multipliers on Schatten–von-Neumann–Orlicz classes. Four applications are given: lacunary sets, unconditional Schauder bases for the subspace of a Lebesgue space determined by a given spectrum $\Lambda \,\subseteq \,\Gamma$, the norm of the Hilbert transformand the Riesz projection on Schatten–von-Neumann classes with exponent a power of 2, and the norm of Toeplitz Schur multipliers on Schatten–von-Neumann classes with exponent less than 1.

The non-archimedean power series spaces, ${{A}_{1}}(a)\,\text{and}\,{{A}_{\infty }}(b)$, are the best known and most important examples of non-archimedean nuclear Fréchet spaces. We prove that the range of every continuous linear map from ${{A}_{p}}(a)\,\text{to}\,{{A}_{q}}(b)$ has a Schauder basis if either $p\,=\,1$ or $p\,=\,\infty $ and the set ${{M}_{b,a}}$ of all bounded limit points of the double sequence (${{({{b}_{i}}/{{a}_{j}})}_{i,j\in \mathbb{N}}}$ is bounded. It follows that every complemented subspace of a power series space ${{A}_{p}}(a)$ has a Schauder basis if either $p\,=\,1$ or $p\,=\,\infty $ and the set ${{M}_{a,a}}$ is bounded.