Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-05T06:44:48.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Low Frequency Estimates for Long Range Perturbations in Divergence Form

Published online by Cambridge University Press:  20 November 2018

Jean-Marc Bouclet
Jean-Marc Bouclet*
Affiliation:
Institut de Mathématiques de Toulouse, Université de Toulouse, Toulouse, France, F-31062 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a uniformcontrol as 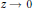$z\,\to \,0$ for the resolvent 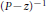${{(P-z)}^{-1}}$ of long range perturbations $P$ of the Euclidean Laplacian in divergence form by combining positive commutator estimates and properties of Riesz transforms. These estimates hold in dimension 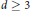$d\,\ge \,3$ when $P$ is defined on 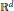${{\mathbb{R}}^{d}}$ and in dimension 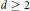$d\,\ge \,2$ when $P$ is defined outside a compact obstacle with Dirichlet boundary conditions.

Keywords

35P25resolvent estimatesthresholdsscattering theoryRiesz transform
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 5 , 18 October 2011 , pp. 961 - 991
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Agmon, S., Spectral properties of Schrödinger operators and scattering theory. Ann. Scuola Norm. Pisa Cl. Sci.(4) 2(1975), no. 2, 151–218.Google Scholar
[2] Aronson, D. G., Non-negative solutions of linear parabolic equations. Ann. Scuola Norm. Sup. Pisa (3) 22(1968), 607–694.Google Scholar
[3] Auscher, P., On necessary and sufficient conditions for L p -estimates of Riesz transforms associated to elliptic operators on R n and related estimates. Mem. Amer. Math. Soc. 186(2007), no. 871.Google Scholar
[4] Bony, J.-F. and D. Häfner, The semilinear wave equation on asymptotically euclidean manifolds. Comm. Partial Differential Equations 35(2010), no. 1, 23–67. doi:10.1080/03605300903396601Google Scholar
[5] Bony, J.-F. and D. Häfner, Low frequency resolvent estimates for long range perturbations of the Euclidean Laplacian. Math. Res. Lett. 17(2010), no. 2, 303–308.Google Scholar
[6] Bouclet, J.-M. and N. Tzvetkov, On global Strichartz estimates for non trapping metrics. J. Funct. Anal. 254(2008), no. 6, 1661–1682. doi:10.1016/j.jfa.2007.11.018Google Scholar
[7] Burq, N., Décroissance de l’énergie locale de l’équation des ondes pour le probl ème ext érieur et absence de r ésonance au voisinage du r éel. Acta Math. 180(1998), no. 1, 1–29. doi:10.1007/BF02392877Google Scholar
[8] Burq, N., Semi-classical estimates for the resolvent in non trapping geometries. Int. Math. Res. Not. 2002, no. 5, 221–241.Google Scholar
[9] Cardoso, F. and G. Vodev, Uniform estimates of the resolvent of the Laplace-Beltrami operator on infinite volume Riemannian manifolds. II. Ann. Henri Poincar é 3(2002), no. 4, 673–691. doi:10.1007/s00023-002-8631-8Google Scholar
[10] Carron, G., Le saut en z éro de la fonction de d écalage spectral. J. Funct. Anal. 254(2004), no. 1, 222–260. doi:10.1016/j.jfa.2003.07.013Google Scholar
[11] Carron, G., T. Coulhon, and A. Hassell, Riesz transform and Lp-cohomology for manifolds with Euclidean ends. Duke Math. J. 133(2006), no. 1, 59–93. doi:10.1215/S0012-7094-06-13313-6Google Scholar
[12] Christiansen, T., Weyl asymptotics for the Laplacian on asymptotically Euclidean spaces. Amer. J. Math. 121(1999), no. 1, 1–22. doi:10.1353/ajm.1999.0009Google Scholar
[13] Davies, E. B., Heat kernels and spectral theory. Cambridge Tracts in Mathematics, 92, Cambridge University Press, , 1989.Google Scholar
[14] Derezinski, J. and E. Skibsted, Quantum scattering at low energies. J. Funct. Anal. 257(2009), no. 6, 1828–1920. doi:10.1016/j.jfa.2009.05.026Google Scholar
[15] Dimassi, M. and J. Sjöstrand, Spectral asymptotics in the semi-classical limit. London Mathematical Society Lecture Note Series, 268, Cambridge University Press, Cambridge, 1999.Google Scholar
[16] Fournais, S. and E. Skibsted, Zero energy asymptotics of the resolvent for a class of slowly decaying potentials. Math. Z. 248(2004), no. 3, 593–633. doi:10.1007/s00209-004-0673-9Google Scholar
[17] Gérard, C., A proof of the abstract limiting absorption principle by energy estimates. J. Funct. Anal. 254(2008), no. 11, 2707–2724. doi:10.1016/j.jfa.2008.02.015Google Scholar
[18] Gérard, C. and A. Martinez, Principe d’absorption limite pour les op érateurs de Schrödinger à longue port ée. C. R. Acad. Sci. Paris S ér. I Math. 306(1988), no. 3, 121–123.Google Scholar
[19] Golénia, S. and T. Jecko, A new look at Mourre’s commutator theory. Complex Anal. Oper. Theory 1(2007), no. 3, 399–422. doi:10.1007/s11785-007-0011-4Google Scholar
[20] Guillarmou, C. and A. Hassell, Resolvent at low energy and Riesz transform for Schrödinger operators on asymptotically conic manifolds. I. Math. Ann. 341(2008), no. 4, 859–896. doi:10.1007/s00208-008-0216-5Google Scholar
[21] Guillarmou, C. and A. Hassell, Resolvent at low energy and Riesz transform for Schrödinger operators on asymptotically conic manifolds. II. Ann. Inst. Fourier 59(2009), no. 4, 1553–1610.Google Scholar
[22] Jensen, A. and T. Kato, Spectral properties of Schrödinger operators and time-decay of the wave functions. Duke Math. J. 46(1979), no. 3, 583–611. doi:10.1215/S0012-7094-79-04631-3Google Scholar
[23] Jensen, A. and G. Nenciu, A unified approach to resolvent expansions at thresholds. Rev. Math. Phys. 13(2001), no. 6, 717–754. doi:10.1142/S0129055X01000843Google Scholar
[24] Koch, H. and D. Tataru, Carleman estimates and absence of embedded eigenvalues. Commun. Math. Phys. 267(2006), no. 2, 419–449. doi:10.1007/s00220-006-0060-yGoogle Scholar
[25] Murata, M., Asymptotic expansion in time for solutions of Schrödinger-type equations. J. Funct. Anal. 49(1982), no. 1, 10–56. doi:10.1016/0022-1236(82)90084-2Google Scholar
[26] Morawetz, C. S., Decay of solutions of the exterior problem for the wave equation. Comm. Pure Appl. Math. 28(1975), 229–264. doi:10.1002/cpa.3160280204Google Scholar
[27] Mourre, E., Absence of singular continuous spectrum for certain selfadjoint operators. Comm. Math. Phys. 78(1980/81), no. 3, 391–408. doi:10.1007/BF01942331Google Scholar
[28] Nakamura, S., Low energy asymptotics for Schrödinger operators with slowly decreasing potentials. Comm. Math. Phys. 161(1994), no. 1, 63–76. doi:10.1007/BF02099413Google Scholar
[29] Perry, P., I. M. Sigal, and B. Simon, Spectral analysis of N-body Schrödinger operators. Ann. of Math. 114(1981), no. 3, 519–567. doi:10.2307/1971301Google Scholar
[30] Robert, D., Asymptotique de la phase de diffusion à haute énergie pour des perturbations du second ordre du laplacien. Ann. Sci. École Norm. Sup. (4) 25(1992), no. 2, 107–134.Google Scholar
[31] Tataru, D., Parametrices and dispersive equations for Schrödinger operators with variable coefficients. Amer. J. Math. 130(2008), no. 3, 571–634. doi:10.1353/ajm.0.0000Google Scholar
[32] Vasy, A. and M. Zworski, Semiclassical estimates in asymptotically Euclidean scattering. Comm. Math. Phys. 212(2000), no. 1, 205–217. doi:10.1007/s002200000207Google Scholar
[33] Wang, X. P., Time-decay of scattering solutions and classical trajectories. Ann. Inst. H. Poincar é Phys. Th éor. 47(1987), no. 1, 25–37.Google Scholar
[34] Wang, X. P., Asymptotic behavior of resolvent for N-body Schrödinger operarors near a threshold. Ann. Henri Poincar é 4(2003), no. 3, 553–600. doi:10.1007/s00023-003-0139-3Google Scholar
[35] Wang, X. P., Asymptotic expansion in time of the Schrödinger group on conical manifolds. Ann. Inst. Fourier 56(2006), no. 6, 1903–1945.Google Scholar
[36] Yafaev, D., Spectral properties of the Schrödinger operator with positive slowly decreasing potential. (Russian) Funktsional. Anal. i Prilozhen. 16(1982), no. 4, 47–54, 96. doi:10.1007/BF01081809Google Scholar