Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:20:29.374Z Has data issue: false hasContentIssue false
  • English
  • Français

On Complemented Subspaces of Non-Archimedean Power Series Spaces

Published online by Cambridge University Press:  20 November 2018

Wiesław Śliwa  and
Agnieszka Ziemkowska
Wiesław Śliwa
Affiliation:
Faculty of Mathematics and Computer Science, A. Mickiewicz University, ul. Umultowska 87, 61-614 Poznań, Poland email: [email protected]@amu.edu.pl
Agnieszka Ziemkowska
Affiliation:
Faculty of Mathematics and Computer Science, A. Mickiewicz University, ul. Umultowska 87, 61-614 Poznań, Poland email: [email protected]@amu.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The non-archimedean power series spaces, ${{A}_{1}}(a)\,\text{and}\,{{A}_{\infty }}(b)$, are the best known and most important examples of non-archimedean nuclear Fréchet spaces. We prove that the range of every continuous linear map from ${{A}_{p}}(a)\,\text{to}\,{{A}_{q}}(b)$ has a Schauder basis if either $p\,=\,1$ or 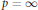$p\,=\,\infty $ and the set ${{M}_{b,a}}$ of all bounded limit points of the double sequence (${{({{b}_{i}}/{{a}_{j}})}_{i,j\in \mathbb{N}}}$ is bounded. It follows that every complemented subspace of a power series space ${{A}_{p}}(a)$ has a Schauder basis if either $p\,=\,1$ or 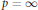$p\,=\,\infty $ and the set ${{M}_{a,a}}$ is bounded.

Keywords

46S1047S1046A35non-archimedean Köthe spacerange of a continuous linear mapSchauder basis
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 5 , 18 October 2011 , pp. 1188 - 1200
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] De Grande-De Kimpe, N., Non-Archimedean Fréchet spaces generalizing spaces of analytic functions. Nederl. Akad. Wetensch. Indag. Mathem. 44(1982), 423–439.Google Scholar
[2] De Grande-De Kimpe, N. and C. Perez-Garcia, Weakly closed subspaces and the Hahn-Banach extension property in p-adic analysis. Nederl. Akad. Wetensch. Indag. Mathem. 50(1988), no. 3, 253–261.Google Scholar
[3] De Grande-De Kimpe, N., J. Kąkol, C. Perez-Garcia, and W. H. Schikhof, p-adic locally convex inductive limits. In: p-adic Functional Analysis. Lecture Notes in Pure and Appl. Math. 192, Dekker, New York, 1997, pp. 159–222.Google Scholar
[4] De Grande-De Kimpe, N., J. Kąkol, C. Perez-Garcia, and W. H. Schikhof, Orthogonal sequences in non-Archimedean locally convex spaces. Indag. Mathem. (N.S.) 11(2000), no. 2, 187–195. doi:10.1016/S0019-3577(00)89076-XGoogle Scholar
[5] De Grande-De Kimpe, N., J. Kąkol, C. Perez-Garcia, and W. H. Schikhof, Orthogonal and Schauder bases in non-Archimedean locally convex spaces. In: p-adic Functional Analysis. Lecture Notes in Pure and Appl. Math. 222, Dekker, New York, 2001, pp. 103–126.Google Scholar
[6] Dubinsky, E., and D. Vogt, Complemented subspaces in tame power series spaces. Studia Math. 93(1988), no. 1, 71–85.Google Scholar
[7] K, A.. Katsaras, On non-Archimedean sequences spaces. Bull. Inst. Math. Acad. Sinica 18(1990), no. 2, 113–126.Google Scholar
[8] Krone, J., Existence of bases and the dual splitting relation for Fréchet spaces. Studia Math. 92(1989), no. 1, 37–48.Google Scholar
[9] Perez, C.-Garcia, Locally convex spaces over non-Archimedean valued fields. In: Ultrametric Functional Analysis, Contemporary Math. 319, American Mathematical Society, Providence, RI, 2003, pp. 251–279.Google Scholar
[10] van Rooij, A.C.M. , Non-Archimedean functional analysis. Monographs and Textbooks in Pure and Applied Math. 51, Marcel Dekker, New York, 1978.Google Scholar
[11] Schikhof, W. H., Locally convex spaces over nonspherically complete valued fields. Bull. Soc. Math. Belg. Sér. B 38(1986), no. 2, 187–224.Google Scholar
[12] Schikhof, W. H., Topological stability of p-adic compactoids under continuous injections. Report 8644, 1986, Department of Mathematics Catholic University, Nijmegen, The Netherlands, pp. 1–22.Google Scholar
[13] Schikhof, W. H., Minimal Hausdorff p-adic locally convex spaces. Ann. Math. Blaise Pascal 2(1995), no. 1, 259–266.Google Scholar
[14] Śliwa, W., Examples of non-Archimedean nuclear Fréchet spaces without a Schauder basis. Indag. Mathem. (N.S.) 11(2000), no. 4, 607–616. doi:10.1016/S0019-3577(00)80029-4Google Scholar
[15] Śliwa, W., Closed subspaces without Schauder bases in non-Archimedean Fréchet spaces. Indag. Mathem. (N.S.) 12 (2001), no. 2, 261–271. doi:10.1016/S0019-3577(01)80031-8Google Scholar
[16] Śliwa, W., On the quasi-equivalence of orthogonal bases in non-Archimedean metrizable locally convex spaces. Bull. Belg. Math. Soc. Simon Stevin 9(2002), no. 3, 465–472.Google Scholar
[17] Śliwa, W., Every non-normable non-Archimedean Köthe space has a quotient without the bounded approximation property. Indag. Mathem. (N.S.) 15(2004), no. 4, 579–587. doi:10.1016/S0019-3577(04)80020-XGoogle Scholar
[18] Śliwa, W., On relations between non-Archimedean power series spaces. Indag. Mathem. (N.S.) 17(2006), no. 4, 627–639. doi:10.1016/S0019-3577(06)81038-4Google Scholar