A subset S of a topological space X is z-embedded in X in case each zero-set of S is the restriction to S of a zero-set of X. (A zero-set is the set of zeros of a real-valued continuous function.) For the basic theory of z-embedding, see [3] and [4] (and see [4] for a comprehensive bibliography of relevant papers).

In an interesting, but apparently largely unknown, paper [1] Halin has introduced the concept of a primitive set of vertices of a graph. This concept, or rather a slight modification of it, seems to provide the key to a new approach to the wrell-known and important class of graph-theoretical problems centering on the notion of separation. As is well known, if A, B, C are sets of vertices of a (non-oriented) graph X, C is said to separate A and B if and only if every AB-path in X contains a vertex of C.

L'objet de cet article est essentiellement de poursuivre la généralisation entreprise par Sabidussi [4] du concept d'ensemble primitif de sommets d'un graphe, introduit par Halin [1].

N. Wiener [12] introduced the idea of the class Vp. A 2 π-periodic function ƒ is said to have bounded p-variation Vp(f)(1 ≦ p < ∞), or to belong to the class Vp, if

Let R be a commutative ring with an identity. An ideal A of R is called a multiplication ideal if for every ideal B ⊆ A there exists an ideal C such that B = AC. A ring R is called a multiplication ring if all its ideals are multiplication ideals. A ring R is called an almost multiplication ring if RM is a multiplication ring for every maximal ideal M of R. Multiplication rings and almost multiplication rings have been extensively studied—for example, see [4; 8; 9; 11; 12; 15; and 16].

Consider the biaxially symmetric potential equation

where α, β > — 1/2. If 2α + 1 and 2 β + 1 are non-negative integers and if X corresponds to the hypercircle

then the biaxisymmetric Laplace equation in E2(α+ β+2),

and (1.1) are equivalent.

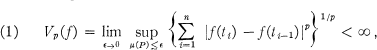
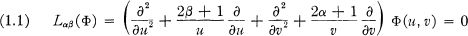
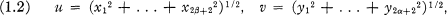
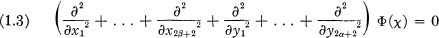
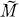For a field M we denote by Ms and respectively the separable closure and the algebraic closure of M. If F is a variety which is defined over 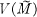M, then we denote by V(M) the set of all if-rational points of V. M is said to be pseudo-algebraically closed (PAC) field, if V(M) ≠ θ for every non-void abstract variety V defined over M. It can be shown that then is dense in V(M) in the Zariski M -topology.

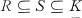Let R be a (commutative integral) domain having quotient field K. A domain S satisfying , is called an 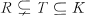overring of R. We say R has a minimal overring T, in case and there are no domains properly between R and T. The purpose of this paper is the study of certain classes of coherent domains having local minimal overrings; that is, having minimal overrings with unique maximal ideals.

The theory of non-increasing (decreasing) equimeasurable rearrangements of functions was introduced by Hardy and Littlewood [6] in connection with their studies of fractional integrals and integral operators. Elementary properties of equimeasurable decreasing rearrangements are given in the monograph [7] of Hardy, Littlewood, and Polya on inequalities, while a more recent treatment is Okikiolu [9, § 5.4].

A Fuchsian group G is a discrete group of fractional linear transforms each of which preserve a disc (or half plane). We consider only groups which preserve the unit disc Δ = {z: |z| < 1} and none of whose transforms, except the identity, fix infinity (any Fuchsian group is conjugate to such a group).

In this paper we study conditions under which certain localizations of semilocal Hi and Di rings satisfy the second chain condition. Two of these results are as follows.

• 1) If P is a prime in a semilocal Hi ring with depth P > i ≧ height P — 1, then RP satisfies the second chain condition.

  2) If P is a prime in a semilocal Dt ring with depth P ≧ i, then RP satisfies the second chain condition.

Let Specie denote the set of prime ideals of a commutative ring with identity R, ordered by inclusion; and call a partially ordered set spectral if it is order isomorphic to Spec R for some R. What are some conditions, necessary or sufficient, for a partially ordered set X to be spectral? The most desirable answer would be the type of result that would allow one to stare at the diagram of a given X and then be able to say whether or not X is spectral. For example, it is known that finite partially ordered sets are spectral (see [2] or [5]).

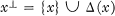The stacking method (see [1] and [5, Section 6]) has been used with great success in ergodic theory to construct a wide variety of examples of ergodic transformations (see, for example, [1 ; 3 ; 4; 5; 7]). However very little is known in general about the class of transformations which can be constructed by the stacking method using single stacks. In particular there is no simple characterization of the class .

In this paper we are concerned with the fourth order nonlinear differential equation

where the following conditions are always assumed to hold:

(a) r(t) is continuous and positive for t ≠ 0, and

Suppose we have n events Ai, … , An and let p(Aj1 … , Ajk) be the probability that the events Ah, . . . , Ajk occur jointly. The probability P0 that none of Ai, . . . , An occur is given by Poincaré's formula, the probabilistic version of the principle of inclusion and exclusion:

A regular T1 space is said to be R-closed if there is no regular T1 space in which it can be embedded as a nonclosed subspace. A regular T1 space is said to be minimal regular if no regular T1 topology on the underlying set is strictly weaker than the given topology. It is known (see [1, Theorem 4, p. 455]) that every minimal regular space is R-closed. An R-closed space, however, need not be minimal regular [3, Example 2, p. 288].

A combinatorial interpretation of Schur functions in terms of Young tableaux is well-known. (For example, see Littlewood [1] or Thomas [4]). The purpose of this paper is to present a combinatorial interpretation of the wreath product (or plethysm) of two Schur functions.

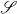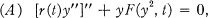
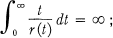
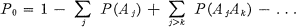
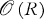Let denote the space of functions holomorphic on an open Riemann surface 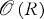R, where has the topology of uniform convergence on compact sets. In this note, we characterize the dual space *. The result is not new, for it is implicitly contained in the more general results of Tillmann [5] and, in case R is planar, in those of Köthe [4]. However, the paper of Gunning and Narasimhan [3], which appeared subsequently, allows us to give a short proof of this important result. Actually, our characterization is a natural one in terms of differentials, while the Köthe-Tillmann characterization is in terms of functions, but we show that these two characterizations are isomorphic. We end our paper by using our characterization to prove an interpolation result. The second author gratefully acknowledges a helpful discussion with Professor George Szekeres.

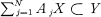Consider a system of N linear transformations A1, … , AN: V → W, where F and IF are complex vector spaces. Denote it for short by (F, W). A pair of subspaces X ⊂ V, Y ⊂ W such that determines a subsystem (X, Y) and a quotient system (V/X, W/Y) (with the induced transformations). The subsystem (X, Y) is of finite codimension in (V, W) if and only if V/X and W / Y are finite-dimensional. It is a direct summand of (V, W) in case there exist supplementary subspaces P of X in F and Q of F in IF such that (P, Q) is a subsystem.