Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T06:41:42.891Z Has data issue: false hasContentIssue false
  • English
  • Français

Purity And Copurity in Systems of Linear Transformations

Published online by Cambridge University Press:  20 November 2018

Frank Zorzitto
Frank Zorzitto*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider a system of N linear transformations A1, … , AN: V → W, where F and IF are complex vector spaces. Denote it for short by (F, W). A pair of subspaces X ⊂ V, Y ⊂ W such that 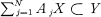determines a subsystem (X, Y) and a quotient system (V/X, W/Y) (with the induced transformations). The subsystem (X, Y) is of finite codimension in (V, W) if and only if V/X and W / Y are finite-dimensional. It is a direct summand of (V, W) in case there exist supplementary subspaces P of X in F and Q of F in IF such that (P, Q) is a subsystem.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 28 , Issue 4 , 01 August 1976 , pp. 889 - 896
Copyright
Copyright © Canadian Mathematical Society 1976

References

1. Aronszajn, N., Quadratic forms on vector spaces, Proc. Intern. Symposium on Linear Spaces 1960 (Jerusalem, 1961).Google Scholar
2. Aronszajn, N. and Fixman, U., Algebraic spectral problems, Studia Math. 30 (1968), 273–338.Google Scholar
3. Fixman, U., On algebraic equivalence between pairs of linear transformations, Trans. Amer. Math. Soc. 113 (1964), 424–453.Google Scholar
4. Fixman, U. and Zorzitto, F., Direct summands of systems of continuous linear transformations, Queen's University Math, preprint, 1975.Google Scholar
5. Fixman, U. and Zorzitto, F., A purity criterion for pairs of linear transformations, Can. J. Math. 26 (1974), 734–745.Google Scholar
6. Robertson, A. P. and Robertson, W. J., Topological vector spaces (Cambridge Univ. Press, Cambridge, 1964).Google Scholar
7. Zorzitto, F., Topological decompositions in systems of linear transformations, Ph.D. thesis, Queen's University, Kingston, Ontario, 1972.Google Scholar