Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zafrullah, Muhammad
1978.
On finite conductor domains.
Manuscripta Mathematica,
Vol. 24,
Issue. 2,
p.
191.
Sato, Junro
Sugatani, Takasi
and
Yoshida, Ken-ichi
1992.
On minimal overrings of a noetherian domain.
Communications in Algebra,
Vol. 20,
Issue. 6,
p.
1735.
Ayache, Ahmed
2003.
Minimal Overrings of an Integrally Closed Domain.
Communications in Algebra,
Vol. 31,
Issue. 12,
p.
5693.
Picavet, Gabriel
and
Picavet-L’Hermitte, Martine
2006.
Multiplicative Ideal Theory in Commutative Algebra.
p.
369.
Dobbs, David E.
and
Shapiro, Jay
2006.
A classification of the minimal ring extensions of an integral domain.
Journal of Algebra,
Vol. 305,
Issue. 1,
p.
185.
Dobbs, David E.
2006.
Every Commutative Ring Has a Minimal Ring Extension.
Communications in Algebra,
Vol. 34,
Issue. 10,
p.
3875.
Picozza, Giampaolo
and
Tartarone, Francesca
2008.
When the Semistar Operation is the Identity.
Communications in Algebra,
Vol. 36,
Issue. 5,
p.
1954.
Dorsey, Thomas J.
and
Mesyan, Zachary
2009.
On Minimal Extensions of Rings.
Communications in Algebra,
Vol. 37,
Issue. 10,
p.
3463.
Kumar, Rahul
and
Gaur, Atul
2018.
On λ-extensions of commutative rings.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 04,
p.
1850063.
Kumar, Rahul
and
Gaur, Atul
2018.
Δ-Extension of rings and invariance properties of ring extension under group action.
Journal of Algebra and Its Applications,
Vol. 17,
Issue. 12,
p.
1850239.
Kumar, Rahul
and
Gaur, Atul
2021.
Pointwise maximal subrings.
Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry,
Vol. 62,
Issue. 4,
p.
843.
Kim, Hwankoo
and
Tamoussit, Ali
2022.
Integral domains issued from associated primes.
Communications in Algebra,
Vol. 50,
Issue. 2,
p.
538.
Guerrieri, Lorenzo
and
Loper, K. Alan
2024.
Non-integrally closed Kronecker function rings and integral domains with a unique minimal overring.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 203,
Issue. 4,
p.
1483.


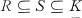 , is called an
, is called an 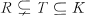 and there are no domains properly between
and there are no domains properly between 