Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lemańczyk, Mariusz
1985.
The rank of regular morse dynamical systems.
Probability Theory and Related Fields,
Vol. 70,
Issue. 1,
p.
33.
Connes, A.
and
Woods, E. J.
1985.
Approximately transitive flows and ITPFI factors.
Ergodic Theory and Dynamical Systems,
Vol. 5,
Issue. 2,
p.
203.
King, Jonathan
1986.
The commutant is the weak closure of the powers, for rank-1 transformations.
Ergodic Theory and Dynamical Systems,
Vol. 6,
Issue. 3,
p.
363.
Golodets, B. Ya.
and
Sokhet, A. M.
1990.
Ergodic actions of Abelian groups with a discrete spectrum, and approximate transitivity.
Journal of Soviet Mathematics,
Vol. 52,
Issue. 6,
p.
3530.
Iwanik, A.
1994.
Cyclic approximation of irrational rotations.
Proceedings of the American Mathematical Society,
Vol. 121,
Issue. 3,
p.
691.
Ferenczi, Sébastien
1996.
Rank and symbolic complexity.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 4,
p.
663.
De La Rue, Thierry
1996.
Systèmes dynamiques gaussiens d'entropie nulle, lâchement et non lâchement Bernoulli.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
379.
Berthé, Valérie
Chekhova, Nataliya
and
Ferenczi, Sébastien
1999.
Covering numbers: Arithmetics and dynamics for rotations and interval exchanges.
Journal d'Analyse Mathématique,
Vol. 79,
Issue. 1,
p.
1.
Chekhova, Nataliya
2000.
Covering numbers of rotations.
Theoretical Computer Science,
Vol. 230,
Issue. 1-2,
p.
97.
Ageev, Oleg
2005.
Spectral rigidity of group actions: Applications to the case gr⟨𝑡,𝑠;𝑡𝑠=𝑠𝑡²⟩.
Proceedings of the American Mathematical Society,
Vol. 134,
Issue. 5,
p.
1331.
Lemańczyk, Mariusz
2009.
Encyclopedia of Complexity and Systems Science.
p.
8554.
Lemańczyk, Mariusz
2012.
Mathematics of Complexity and Dynamical Systems.
p.
1618.
DANILENKO, ALEXANDRE I.
2013.
A survey on spectral multiplicities of ergodic actions.
Ergodic Theory and Dynamical Systems,
Vol. 33,
Issue. 1,
p.
81.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2020.
Encyclopedia of Complexity and Systems Science.
p.
1.
ARBULÚ, FELIPE
and
DURAND, FABIEN
2023.
Dynamical properties of minimal Ferenczi subshifts.
Ergodic Theory and Dynamical Systems,
Vol. 43,
Issue. 12,
p.
3923.
Drillick, Hindy
Espinosa-Dominguez, Alonso
Jones-Baro, Jennifer N.
Leng, James
Mandelshtam, Yelena
and
Silva, Cesar E.
2023.
Non-rigid rank-one infinite measures on the circle.
Dynamical Systems,
Vol. 38,
Issue. 2,
p.
275.
Kanigowski, Adam
and
Lemańczyk, Mariusz
2023.
Ergodic Theory.
p.
109.
Koltai, Péter
and
Kunde, Philipp
2024.
A Koopman–Takens Theorem: Linear Least Squares Prediction of Nonlinear Time Series.
Communications in Mathematical Physics,
Vol. 405,
Issue. 5,
CORREIA, CORENTIN
2024.
Rank-one systems, flexible classes and Shannon orbit equivalence.
Ergodic Theory and Dynamical Systems,
p.
1.
DANILENKO, ALEXANDRE I.
and
VIEPRIK, MYKYTA I.
2025.
Rank-one non-singular actions of countable groups and their odometer factors.
Ergodic Theory and Dynamical Systems,
Vol. 45,
Issue. 4,
p.
1078.


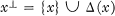 of transformations which can be constructed by the stacking method using single stacks. In particular there is no simple characterization of the class
of transformations which can be constructed by the stacking method using single stacks. In particular there is no simple characterization of the class 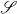 .
.