Research Article
Testing on null sequences is enough for Bochner integrability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-307
-
- Article
-
- You have access
- Export citation
On weak Hadamard differentiability of convex functions on Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-166
-
- Article
-
- You have access
- Export citation
An algorithm for constructing locally optimal min-max triangulation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 167-176
-
- Article
-
- You have access
- Export citation
On the growth of fundamental groups of nonpositive curvature manifolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 483-487
-
- Article
-
- You have access
- Export citation
Dimensions of spaces of Siegel modular forms of low weight in degree four
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 309-315
-
- Article
-
- You have access
- Export citation
Some existence theorems for differential inclusions in Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-327
-
- Article
-
- You have access
- Export citation
Enriched accessible categories
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 489-501
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 54 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 54 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On the range of the Y-transform
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-345
-
- Article
-
- You have access
- Export citation
On the ring of locally bounded Nash meromorphic functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 503-507
-
- Article
-
- You have access
- Export citation
Higher-order optimality conditions for a minimax
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 509-516
-
- Article
-
- You have access
- Export citation
Class two nilpotent capable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 347-352
-
- Article
-
- You have access
- Export citation
On the cohomology of a class of nilpotent Lie algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 517-527
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 54 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 54 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 54 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 54 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

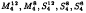 using Erokhin's work on Niemeier lattices and geometric methods involving the hyperelliptic locus.
using Erokhin's work on Niemeier lattices and geometric methods involving the hyperelliptic locus.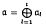 induced by
induced by