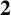 $\mathbf {2}$
$\mathbf {2}$
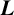 $\boldsymbol {L}$
-VALUE
$\boldsymbol {L}$
-VALUE
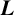 $\boldsymbol {L}$
-FUNCTIONS
$\boldsymbol {L}$
-FUNCTIONS
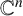 $\mathbb {C}^n$
$\mathbb {C}^n$