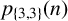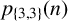Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rahman, Riyajur
and
Saikia, Nipen
2022.
Arithmetic properties of 5-regular partition in three and five colours.
The Journal of Analysis,
Vol. 30,
Issue. 4,
p.
1427.