Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T08:09:03.427Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF 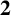$\mathbf {2}$

Part of: Elementary number theory Combinatorics

Published online by Cambridge University Press:  14 March 2022

CHAO HUANG Open the ORCID record for CHAO HUANG [Opens in a new window]  and
HAO PAN Open the ORCID record for HAO PAN [Opens in a new window]
CHAO HUANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, People’s Republic of China e-mail: [email protected]
HAO PAN*
Affiliation:
School of Applied Mathematics, Nanjing University of Finance and Economics Nanjing 210023, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

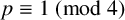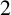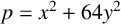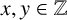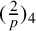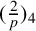Let p be a prime with $p\equiv 1\pmod {4}$ . Gauss first proved that $2$ is a quartic residue modulo p if and only if $p=x^2+64y^2$ for some $x,y\in \Bbb Z$ and various expressions for the quartic residue symbol $(\frac {2}{p})_4$ are known. We give a new characterisation via a permutation, the sign of which is determined by $(\frac {2}{p})_4$ . The permutation is induced by the rule 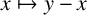$x \mapsto y-x$ on the 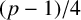$(p-1)/4$ solutions 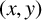$(x,y)$ to 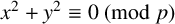$x^2+y^2\equiv 0 \pmod {p}$ satisfying 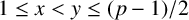$1\leq x < y \leq (p-1)/2$ .

Keywords

quartic residuepermutationclass number

MSC classification

Primary: 11A15: Power residues, reciprocity
Secondary: 05A05: Permutations, words, matrices 11A07: Congruences; primitive roots; residue systems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 1 , August 2022 , pp. 1 - 6
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the National Natural Science Foundation of China (Grant No.11971222). The second author is supported by the National Natural Science Foundation of China (Grant No.12071208).

References

Barrucand, P. and Cohn, H., ‘Note on primes of type ${x}^2+32{y}^2$ , class number and residuacity’, J. reine angew. Math. 238 (1969), 67–70.Google Scholar
Berndt, B. C., Evans, R. J. and Williams, K. S., Gauss and Jacobi Sums (Wiley, New York, 1998).Google Scholar
Conway, J. H., The Sensual (Quadratic) Form, Carus Mathematical Monographs, 26 (The Mathematical Association of America, Washington DC, 1997), 127–132.Google Scholar
Dressler, R. E. and Shult, E. E., ‘A simple proof of the Zolotareff–Frobenius theorem’, Proc. Amer. Math. Soc. 54 (1976), 53–54.Google Scholar
Gauss, C. F., ‘Theoria residuorum biquadraticorum, Commentatio prima’, Comment. Soc. Reg. Gottingensis 6 (1828), 28 pages. [Collected Works, Volume 2, 65–92].Google Scholar
Hasse, H., ‘Über die Klassenzahl des Körper $P\left(\hspace{-2pt}\sqrt{-2p}\right)$ mit einer Primzahl $p\ne 2$ ’, J. Number Theory 1 (1969), 231–234.CrossRefGoogle Scholar
Ireland, K. and Rosen, M., A Classical Introduction to Modern Number Theory, 2nd edn, Graduate Texts in Mathematics, 84 (Springer, New York, 1990).CrossRefGoogle Scholar
Lehmer, E., ‘Generalizations of Gauss’s lemma’, in: Number Theory and Algebra: Collected papers dedicated to Henry B. Mann, Arnold E. Ross, and Olga Taussky-Todd (ed. H. Zassenhaus) (Academic Press, New York, 1977), 187–194.Google Scholar
Pizer, A., ‘On the 2-part of the class number of imaginary quadratic number fields’, J. Number Theory 8 (1976), 184–192.Google Scholar
Williams, K. S., ‘Note on a result of Barrucand and Cohn’, J. reine angew. Math. 285 (1976), 218–220.Google Scholar