Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T08:09:15.768Z Has data issue: false hasContentIssue false
  • English
  • Français

MINIMALLY TRANSITIVE FAMILIES OF SUBSPACES OF 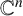$\mathbb {C}^n$

Part of: Basic linear algebra

Published online by Cambridge University Press:  20 January 2022

W. E. LONGSTAFF Open the ORCID record for W. E. LONGSTAFF [Opens in a new window]
W. E. LONGSTAFF*
Affiliation:
11 Tussock Crescent, Elanora, Queensland 4221, Australia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Every transitive family of subspaces of a vector space of finite dimension 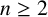$n\ge 2$ over a field 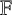$\mathbb {F}$ contains a subfamily which is transitive but has no proper transitive subfamily. Such a subfamily is called minimally transitive. Each has at most 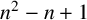$n^2-n+1$ elements. On 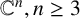${{\mathbb {C}}}^n, n\ge 3$ , a minimally transitive family of subspaces has at least four elements and a minimally transitive family of one-dimensional subspaces has 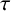$\tau $ elements where 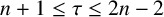$n+1\le \tau \le 2n-2$ . We show how a minimally transitive family of one-dimensional subspaces arises when it consists of the subspaces spanned by the standard basis vectors together with those spanned by 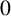$0$ – 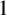$1$ vectors. On a space of dimension four, the set of nontrivial elements of a medial subspace lattice has five elements if it is minimally transitive. On spaces of dimension 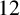$12$ or more, the set of nontrivial elements of a medial subspace lattice can have six or more elements and be minimally transitive.

Keywords

transitiveminimalmedial

MSC classification

Primary: 15A30: Algebraic systems of matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 1 , August 2022 , pp. 70 - 82
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Hadwin, D. W., Longstaff, W. E. and Rosenthal, P., ‘Small transitive lattices’, Proc. Amer. Math. Soc. 87(1) (1983), 121–124.Google Scholar
Halmos, P. R., ‘Ten problems in Hilbert space’, Bull. Amer. Math. Soc. 76 (1970), 887–933.Google Scholar
Lambrou, M. S. and Longstaff, W. E., ‘Small transitive families of subspaces in finite dimensions’, Linear Algebra Appl. 357 (2002), 229–245.Google Scholar
Longstaff, W. E., ‘Small transitive families of dense operator ranges’, Integral Equations Operator Theory 45 (2003), 343–350.Google Scholar
Longstaff, W. E., ‘Small transitive families of subspaces’, Acta Math. Sinica 19(3) (2003), 567–576.Google Scholar