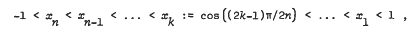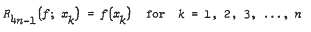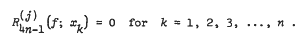Research Article
Some results for the general bulk service queueing system
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-179
-
- Article
-
- You have access
- Export citation
Trees as commutative BCK-Algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-190
-
- Article
-
- You have access
- Export citation
On a theorem of Brudno over non-Archimedian Fields
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 191-194
-
- Article
-
- You have access
- Export citation
A remark on an integral inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 195-197
-
- Article
-
- You have access
- Export citation
Notions of topos
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-208
-
- Article
-
- You have access
- Export citation
Some remarks on symmetry for a monoidal category
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 209-214
-
- Article
-
- You have access
- Export citation
Factorisation of Lipschitz functions on zero dimensional groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 215-225
-
- Article
-
- You have access
- Export citation
A covering property of finite groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-235
-
- Article
-
- You have access
- Export citation
Composition operators and several complex variables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 237-247
-
- Article
-
- You have access
- Export citation
Characterizations of the sphere by the mean II-curvature
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-253
-
- Article
-
- You have access
- Export citation
Weak ideal invariance and orders in Artinian rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-264
-
- Article
-
- You have access
- Export citation
Automatic continuity of positive functionals on topological involution algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 265-281
-
- Article
-
- You have access
- Export citation
On interpolation polynomials of the Hermite-Fejér type II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 283-291
-
- Article
-
- You have access
- Export citation
On exponential dichotomy in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-306
-
- Article
-
- You have access
- Export citation
On rings with nil commutator ideal
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-311
-
- Article
-
- You have access
- Export citation
Some translation planes constructed by multiple derivation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-315
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
Some problems in teletraffic with particular emphasis on limited availability networks
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 317
-
- Article
-
- You have access
- Export citation
Construction and resolution of quadruple systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 319-320
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 23 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 23 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

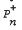 , under equilibrium, have been derived by using the supplementary variable technique. An expression has been derived for the expected value of the queue size and its relation with the expected value of the waiting time of a customer has been explored. A numerical case has been worked out on the assumption that bulk service follows a specified Erlangian distribution.
, under equilibrium, have been derived by using the supplementary variable technique. An expression has been derived for the expected value of the queue size and its relation with the expected value of the waiting time of a customer has been explored. A numerical case has been worked out on the assumption that bulk service follows a specified Erlangian distribution.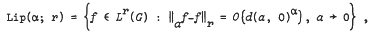
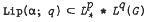 , where 1 ≤
, where 1 ≤ 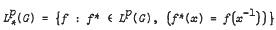 . It is also shown that for
. It is also shown that for