Published online by Cambridge University Press: 17 April 2009
This paper deals with a general bulk service queueing system with one server, for which customers arrive in a Poisson stream and the service is in bulk. The maximum number of customers to be served in one lot is B (capacity), but the server does not start service until A (quorum, less than B) customers have accumulated; and the service time follows a general probability distribution. Probability generating functions of the distributions Pn and 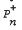 , under equilibrium, have been derived by using the supplementary variable technique. An expression has been derived for the expected value of the queue size and its relation with the expected value of the waiting time of a customer has been explored. A numerical case has been worked out on the assumption that bulk service follows a specified Erlangian distribution.
, under equilibrium, have been derived by using the supplementary variable technique. An expression has been derived for the expected value of the queue size and its relation with the expected value of the waiting time of a customer has been explored. A numerical case has been worked out on the assumption that bulk service follows a specified Erlangian distribution.