The Lachance-Traill, and Lucas-Tooth-Price matrix correction equations/functions for XRF determined concentrations can be graphically interpreted with the help of three dimensional graphics. Statistically derived Lachance-Traill and Lucas-Tooth-Price matrix correction equations can be represented as follows:
1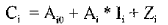
where:
Ci -elemental concentration of element “i”
Ij -X-Ray intensity representing element “i”
Ai0 -regression intercept for element “i”
Ai -regression coefficient
Zj -correction term defined below
2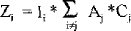
Ai0, Aj , and Zi together represent the results of a multi-dimensional contribution.
li, Ci, and Zi can be represented in three dimensional Cartesian space by X, Y and Z. These three variables are connected by a matrix correction equation that can be graphed as the function Y = F(X, Z), which represents a plane in three dimensional space. It can be seen that each chemical element will deliver a different set of coefficients in the equation of a plane that is called here a calibration plane. The commonly known and used two dimensional calibration plot is a “shadow” of the three dimensional real calibration points. These real (not shadow) points reside on a regression calibration plane in this three dimensional space. Lachance-Traill and Lucas-Tooth-Price matrix correction equations introduce the additional dimension(s) to the two dimensional flat image of uncorrected data. Illustrative examples generated by three dimensional graphics will be presented.