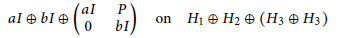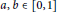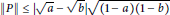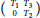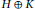Let
 $T$
be a quadratic operator on a complex Hilbert space
$T$
be a quadratic operator on a complex Hilbert space
 $H$
. We show that
$H$
. We show that
 $T$
can be written as a product of two positive contractions if and only if
$T$
can be written as a product of two positive contractions if and only if
 $T$
is of the form
$T$
is of the form
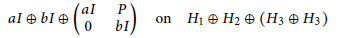 $$aI\,\oplus \,bI\,\oplus \left( \begin{matrix} aI & P \\ 0 & bI \\ \end{matrix} \right)\,\text{on}\,{{H}_{1}}\,\oplus \,{{H}_{2}}\,\oplus \,\left( {{H}_{3\,}}\,\oplus \,{{H}_{3}} \right)$$
$$aI\,\oplus \,bI\,\oplus \left( \begin{matrix} aI & P \\ 0 & bI \\ \end{matrix} \right)\,\text{on}\,{{H}_{1}}\,\oplus \,{{H}_{2}}\,\oplus \,\left( {{H}_{3\,}}\,\oplus \,{{H}_{3}} \right)$$
for some
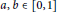 $a,\,b\,\in \,\left[ 0,\,1 \right]$
and strictly positive operator
$a,\,b\,\in \,\left[ 0,\,1 \right]$
and strictly positive operator
 $P$
with
$P$
with
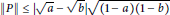 $\left\| P \right\|\,\le \,\left| \sqrt{a}-\sqrt{b} \right|\sqrt{\left( 1-a \right)\left( 1-b \right)}$
. Also, we give a necessary condition for a bounded linear operator
$\left\| P \right\|\,\le \,\left| \sqrt{a}-\sqrt{b} \right|\sqrt{\left( 1-a \right)\left( 1-b \right)}$
. Also, we give a necessary condition for a bounded linear operator
 $T$
with operator matrix
$T$
with operator matrix
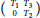 $\left( \begin{matrix}
{{T}_{1}} & {{T}_{3}} \\
0 & {{T}_{2}} \\
\end{matrix} \right)$
on
$\left( \begin{matrix}
{{T}_{1}} & {{T}_{3}} \\
0 & {{T}_{2}} \\
\end{matrix} \right)$
on
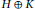 $H\,\oplus \,K$
that can be written as a product of two positive contractions.
$H\,\oplus \,K$
that can be written as a product of two positive contractions.