Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-08T21:37:53.945Z Has data issue: false hasContentIssue false
  • English
  • Français

Factoring a Quadratic Operator as a Product of Two Positive Contractions

Published online by Cambridge University Press:  20 November 2018

Chi-Kwong Li  and
Ming-Cheng Tsai
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William & Mary, Williamsburg, VA 23187, USA e-mail: [email protected]
Ming-Cheng Tsai
Affiliation:
Department of Applied Mathematics, National Sun Yat-sen University, Kaohsiung 80424, Taiwan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $T$ be a quadratic operator on a complex Hilbert space $H$ . We show that $T$ can be written as a product of two positive contractions if and only if $T$ is of the form

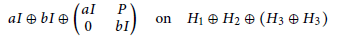$$aI\,\oplus \,bI\,\oplus \left( \begin{matrix} aI & P \\ 0 & bI \\ \end{matrix} \right)\,\text{on}\,{{H}_{1}}\,\oplus \,{{H}_{2}}\,\oplus \,\left( {{H}_{3\,}}\,\oplus \,{{H}_{3}} \right)$$

for some 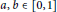$a,\,b\,\in \,\left[ 0,\,1 \right]$ and strictly positive operator $P$ with 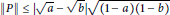$\left\| P \right\|\,\le \,\left| \sqrt{a}-\sqrt{b} \right|\sqrt{\left( 1-a \right)\left( 1-b \right)}$ . Also, we give a necessary condition for a bounded linear operator $T$ with operator matrix 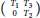$\left( \begin{matrix} {{T}_{1}} & {{T}_{3}} \\ 0 & {{T}_{2}} \\ \end{matrix} \right)$ on 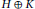$H\,\oplus \,K$ that can be written as a product of two positive contractions.

Keywords

47A6047A6847A63quadratic operatorpositive contractionspectral theorem
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 354 - 362
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Amrein, W. O. and Sinha, K. B., On pairs of projections in a Hilbert space. Linear Algebra Appl. 208/209(1994), 425–435. http://dx.doi.org/10.1016/0024-3795(94)90454-5 Google Scholar
[2] Ballantine, C. S., Products of positive definite matrices. I. Pacific J. Math. 23(1967), 427–433. http://dx.doi.org/10.2140/pjm.1967.23.427 Google Scholar
[3] Ballantine, C. S., Products of positive definite matrices. II. Pacific J. Math. 24(1968), 7–17. http://dx.doi.org/10.2140/pjm.1968.24.7 Google Scholar
[4] Ballantine, C. S., Products of positive definite matrices. III. J. Algebra 10(1968), 174–182. http://dx.doi.org/10.101 6/0021-8693(68)90093-8 Google Scholar
[5] Ballantine, C. S., Products of positive definite matrices. IV. Linear Algebra Appl. 3(1970), 79–114. http://dx.doi.org/10.1016/0024-3795(70)90030-3 Google Scholar
[6] Berberian, S. K., Approximate proper vectors.Proc. Amer. Math. Soc. 13(1962), 111–114. http://dx.doi.org/10.1090/S0002-9939-1962-0133690-8 Google Scholar
[7] Bôttcherand, A. Spitkovsky, I. M., A gentle guide to the basics of two projections theory.Linear Algebra Appl. 432(2010), 1412–1459. http://dx.doi.org/10.1016/j.laa.2009.11.002 Google Scholar
[8] Corach, G. and Maestripieri, A., Products of orthogonal projections and polar decompositions. Linear Algebra Appl. 434(2011), 1594–1609. http://dx.doi.org/10.1016/j.laa.2O10.11.033 Google Scholar
[9] Foias, C. and Frazho, A. E., The commutant lifting approach to interpolation problems.Operator Theory: Advances and Applications, 44, Birkhâuser-Verlag, Basel, 1990.Google Scholar
[10] Fujii, J. I., Fujii, M., Izumino, S., Kubo, F., and Nakamoto, R., Strang's inequality. Math.Japon. 37(1992), no. 3, 479–486.Google Scholar
[11] Halmos, P. R., Two subspaces. Trans. Amer. Math. Soc. 144(1969), 381–389. http://dx.doi.org/10.1090/S0002-9947-1969-0251519-5 Google Scholar
[12] Radjavi, H. and Williams, J. P., Products of self-adjoint operators.Michigan Math. J. 16(1969), 177–185. http://dx.doi.org/10.1307/mmjV1029000220 Google Scholar
[13] Tso, S.-H. and Wu, P. Y., Matricial ranges of quadratic operators. Rocky Mountain J. Math. 29(1999), 1139–1152. http://dx.doi.org/10.1216/rmjm/1181071625 Google Scholar
[14] Wu, P. Y., Products of positive semidefinite matrices.Linear Algebra Appl. 111(1988), 53–61. http://dx.doi.org/10.1016/0024-3795(88)90051-1 Google Scholar
[15] Wu, P. Y., The operator factorization problems. Linear Algebra Appl. 117(1989), 35–63. http://dx.doi.org/!0.1016/0024-3795(89)90546-6 Google Scholar