2 results
ONE-LEVEL DENSITY OF LOW-LYING ZEROS OF QUADRATIC HECKE L-FUNCTIONS OF IMAGINARY QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 29 October 2020, pp. 170-192
- Print publication:
- April 2022
-
- Article
- Export citation
One-Level Density of Low-lying Zeros of Quadratic and Quartic Hecke
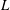 $L$-functions
$L$-functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 427-454
- Print publication:
- April 2020
-
- Article
- Export citation