Article contents
ONE-LEVEL DENSITY OF LOW-LYING ZEROS OF QUADRATIC HECKE L-FUNCTIONS OF IMAGINARY QUADRATIC NUMBER FIELDS
Part of:
Algebraic number theory: global fields
Zeta and $L$-functions: analytic theory
Exponential sums and character sums
Published online by Cambridge University Press: 29 October 2020
Abstract
In this paper, we prove a one level density result for the low-lying zeros of quadratic Hecke L-functions of imaginary quadratic number fields of class number 1. As a corollary, we deduce, essentially, that at least
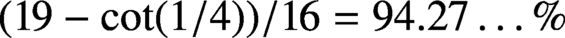 $(19-\cot (1/4))/16 = 94.27\ldots \%$
of the L-functions under consideration do not vanish at 1/2.
$(19-\cot (1/4))/16 = 94.27\ldots \%$
of the L-functions under consideration do not vanish at 1/2.
MSC classification
Primary:
11L40: Estimates on character sums
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Michael Coons
The first-named author was supported in part by NSFC grant 11871082 and the second-named author by the FRG grant PS43707 at UNSW.
References
Alaca, A., Alaca, Ş. and Williams, K. S., ‘Double Gauss sums’, J. Comb. Number Theory 6(2) (2014), 127–153.Google Scholar
Baier, S. and Zhao, L., ‘On the low-lying zeros of Hasse–Weil
 $L$
-functions for elliptic curves’, Adv. Math. 219(3) (2008), 952–985.CrossRefGoogle Scholar
$L$
-functions for elliptic curves’, Adv. Math. 219(3) (2008), 952–985.CrossRefGoogle Scholar
Boylan, H. and Skoruppa, N., ‘Explicit formulas for Hecke Gauss sums in quadratic number fields’, Abh. Math. Semin. Univ. Hambg. 80(2) (2010), 213–226.CrossRefGoogle Scholar
Brumer, A., ‘The average rank of elliptic curves. I’, Invent. Math. 109(3) (1992), 445–472.CrossRefGoogle Scholar
Bui, H. M. and Florea, A., ‘Zeros of quadratic Dirichlet L-functions in the hyperelliptic ensemble’, Trans. Amer. Math. Soc. 370(11) (2018), 8013–8045.10.1090/tran/7317CrossRefGoogle Scholar
Chowla, S., The Riemann Hypothesis and Hilbert’s Tenth Problem, Mathematics and its Applications
, 4 (Gordon and Breach, New York–London–Paris, 1965).Google Scholar
Davenport, H., Multiplicative Number Theory, 3rd edn, Graduate Texts in Mathematics, 74 (Springer, Berlin, 2000).Google Scholar
Dueñez, E. and Miller, S. J., ‘The low lying zeros of a
 $\mathrm{GL}(4)$
and a
$\mathrm{GL}(4)$
and a
 $\mathrm{GL}(6)$
family of
$\mathrm{GL}(6)$
family of
 $L$
-functions’, Compos. Math. 142(6) (2006), 1403–1425.CrossRefGoogle Scholar
$L$
-functions’, Compos. Math. 142(6) (2006), 1403–1425.CrossRefGoogle Scholar
Dueñez, E. and Miller, S. J., ‘The effect of convolving families of
 $L$
-functions on the underlying group symmetries’, Proc. Lond. Math. Soc. (3) 99(3) (2009), 787–820.10.1112/plms/pdp018CrossRefGoogle Scholar
$L$
-functions on the underlying group symmetries’, Proc. Lond. Math. Soc. (3) 99(3) (2009), 787–820.10.1112/plms/pdp018CrossRefGoogle Scholar
Entin, A., Roditty-Gershon, E. and Rudnick, Z., ‘Low-lying zeros of quadratic Dirichlet
 $L$
-functions, hyper-elliptic curves and random matrix theory’, Geom. Funct. Anal. 23(4) (2013), 1230–1261.CrossRefGoogle Scholar
$L$
-functions, hyper-elliptic curves and random matrix theory’, Geom. Funct. Anal. 23(4) (2013), 1230–1261.CrossRefGoogle Scholar
Fouvry, E. and Iwaniec, H., ‘Low-lying zeros of dihedral
 $L$
-functions’, Duke Math. J. 116(2) (2003), 189–217.CrossRefGoogle Scholar
$L$
-functions’, Duke Math. J. 116(2) (2003), 189–217.CrossRefGoogle Scholar
Gao, P., ‘
 $n$
-level density of the low-lying zeros of quadratic Dirichlet
$n$
-level density of the low-lying zeros of quadratic Dirichlet
 $L$
-functions’, Int. Math. Res. Not. 2014(6) (2014), 1699–1728.10.1093/imrn/rns261CrossRefGoogle Scholar
$L$
-functions’, Int. Math. Res. Not. 2014(6) (2014), 1699–1728.10.1093/imrn/rns261CrossRefGoogle Scholar
Gao, P. and Zhao, L., ‘Large sieve inequalities for quartic character sums’, Q. J. Math. 63(4) (2012), 891–917.CrossRefGoogle Scholar
Gao, P. and Zhao, L., ‘Mean values of some Hecke characters’, Acta Arith. 187(2) (2019), 125–141.CrossRefGoogle Scholar
Gao, P. and Zhao, L., ‘One level density of low-lying zeros of quadratic and quartic Hecke
 $L$
-functions’, Canad. J. Math. 72(2) (2020), 427–454.CrossRefGoogle Scholar
$L$
-functions’, Canad. J. Math. 72(2) (2020), 427–454.CrossRefGoogle Scholar
Güloğlu, A. M., ‘Low-lying zeros of symmetric power
 $L$
-functions’, Int. Math. Res. Not. 2005(9) (2005), 517–550.CrossRefGoogle Scholar
$L$
-functions’, Int. Math. Res. Not. 2005(9) (2005), 517–550.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘The average rank of elliptic curves’, Duke Math. J. 122(3) (2004), 225–320.CrossRefGoogle Scholar
Hughes, C. and Miller, S. J., ‘Low-lying zeros of
 $L$
-functions with orthogonal symmetry’, Duke Math. J. 136(1) (2007), 115–172.CrossRefGoogle Scholar
$L$
-functions with orthogonal symmetry’, Duke Math. J. 136(1) (2007), 115–172.CrossRefGoogle Scholar
Hughes, C. P. and Rudnick, Z., ‘Linear statistics of low-lying zeros of
 $L$
-functions’, Q. J. Math. 54(3) (2003), 309–333.CrossRefGoogle Scholar
$L$
-functions’, Q. J. Math. 54(3) (2003), 309–333.CrossRefGoogle Scholar
. Huxley, M. N, ‘Integer points, exponential sums and the Riemann zeta function’, Number Theory for the Millennium III
,
Urbana, IL, 2000 (A. K. Peters, Natick, MA, 2002), 275–290.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, American Mathematical Society Colloquium Publications, 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H., Luo, W. and Sarnak, P., ‘Low lying zeros of families of
 $L$
-functions’, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.10.1007/BF02698741CrossRefGoogle Scholar
$L$
-functions’, Publ. Math. Inst. Hautes Études Sci. 91 (2000), 55–131.10.1007/BF02698741CrossRefGoogle Scholar
Katz, N. and Sarnak, P., ‘Zeros of zeta functions and symmetries’, Bull. Amer. Math. Soc. 36(1) (1999), 1–26.CrossRefGoogle Scholar
Katz, N. and Sarnak, P., Random Matrices, Frobenius Eigenvalues, and Monodromy, American Mathematical Society Colloquium Publications, 45 (American Mathematical Society, Providence, RI, (1999).Google Scholar
Lemmermeyer, F., Reciprocity Laws. From Euler to Eisenstein (Springer, Berlin, 2000).10.1007/978-3-662-12893-0CrossRefGoogle Scholar
. Marshall, S, ‘Zero repulsion in families of elliptic curve L-functions and an observation of Miller’, Bull. Lond. Math. Soc. 45(1) (2013), 80–88.10.1112/blms/bds063CrossRefGoogle Scholar
Mason, A. M. and Snaith, N. C., ‘Orthogonal and symplectic
 $n$
-level densities’, Mem. Amer. Math. Soc. 251(1194) (2018), 93 pp.Google Scholar
$n$
-level densities’, Mem. Amer. Math. Soc. 251(1194) (2018), 93 pp.Google Scholar
Miller, S. J., ‘One- and two-level densities for rational families of elliptic curves: evidence for the underlying group symmetries’, Compos. Math. 140(4) (2004), 952–992.CrossRefGoogle Scholar
Miller, S. J., ‘Investigations of zeros near the central point of elliptic curve
 $L$
-functions’ with an appendix by E. Dueñez, Exp. Math. 15(3) (2006), 257–279.CrossRefGoogle Scholar
$L$
-functions’ with an appendix by E. Dueñez, Exp. Math. 15(3) (2006), 257–279.CrossRefGoogle Scholar
Miller, S. J., ‘A symplectic test of the
 $L$
-functions ratios conjecture’, Int. Math. Res. Not. IMRN 2008(2008), Art. ID rnm146, 36 pp.Google Scholar
$L$
-functions ratios conjecture’, Int. Math. Res. Not. IMRN 2008(2008), Art. ID rnm146, 36 pp.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory. I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, UK, 2007).Google Scholar
Özlük, A. E. and Snyder, C., ‘On the distribution of the nontrivial zeros of quadratic
 $L$
-functions close to the real axis’, Acta Arith. 91(3) (1999), 209–228.CrossRefGoogle Scholar
$L$
-functions close to the real axis’, Acta Arith. 91(3) (1999), 209–228.CrossRefGoogle Scholar
Patterson, S. J., ‘The distribution of general Gauss sums and similar arithmetic functions at prime arguments’, Proc. Lond. Math. Soc. 54(3) (1987), 193–215.CrossRefGoogle Scholar
Ricotta, G. and Royer, E., ‘Statistics for low-lying zeros of symmetric power
 $L$
-functions in the level aspect’, Forum Math. 23(5) (2011), 969–1028.10.1515/form.2011.035CrossRefGoogle Scholar
$L$
-functions in the level aspect’, Forum Math. 23(5) (2011), 969–1028.10.1515/form.2011.035CrossRefGoogle Scholar
Royer, E., ‘Petits zéros de fonctions
 $L$
de formes modulaires’, Acta Arith. 99(2) (2001), 147–172.CrossRefGoogle Scholar
$L$
de formes modulaires’, Acta Arith. 99(2) (2001), 147–172.CrossRefGoogle Scholar
Rubinstein, M. O., ‘Low-lying zeros of
 $L$
-functions and random matrix theory’, Duke Math. J. 209(1) (2001), 147–181.CrossRefGoogle Scholar
$L$
-functions and random matrix theory’, Duke Math. J. 209(1) (2001), 147–181.CrossRefGoogle Scholar
Soundararajan, K., ‘Nonvanishing of quadratic Dirichlet
 $L$
-functions at
$L$
-functions at
 $s=\frac{1}{2}'$
, Ann. of Math. (2) 152(2) (2000), 447–488.CrossRefGoogle Scholar
$s=\frac{1}{2}'$
, Ann. of Math. (2) 152(2) (2000), 447–488.CrossRefGoogle Scholar
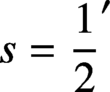 $s=\frac{1}{2}'$
, Ann. of Math. (2) 152(2) (2000), 447–488.CrossRefGoogle Scholar
$s=\frac{1}{2}'$
, Ann. of Math. (2) 152(2) (2000), 447–488.CrossRefGoogle ScholarYoung, M. P., ‘Low-lying zeros of families of elliptic curves’, J. Amer. Math. Soc. 19(1) (2005), 205–250.CrossRefGoogle Scholar
- 1
- Cited by



