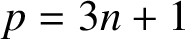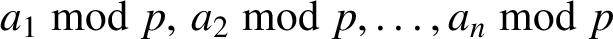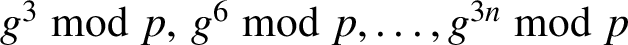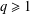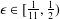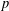5 results
CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 15 July 2021, pp. 188-196
- Print publication:
- April 2022
-
- Article
- Export citation
QUADRATIC NONRESIDUES AND NONPRIMITIVE ROOTS SATISFYING A COPRIMALITY CONDITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 177-183
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
SOME $\mathbb{Z}_{n-1}$ TERRACES FROM $\mathbb{Z}_{n}$ POWER-SEQUENCES, $n$ BEING AN ODD PRIME POWER
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 50 / Issue 3 / October 2007
- Published online by Cambridge University Press:
- 08 January 2008, pp. 527-549
-
- Article
-
- You have access
- Export citation
On Minimal Sets of Generators for Primitive Roots
-
- Journal:
- Canadian Mathematical Bulletin / Volume 38 / Issue 4 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-468
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
Some Remarks on Artin's Conjecture
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 1 / 01 March 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 80-85
- Print publication:
- 01 March 1987
-
- Article
-
- You have access
- Export citation