Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T18:12:48.086Z Has data issue: false hasContentIssue false
  • English
  • Français

CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS

Part of: Elementary number theory Combinatorics Algebraic number theory: global fields

Published online by Cambridge University Press:  15 July 2021

HAI-LIANG WU Open the ORCID record for HAI-LIANG WU [Opens in a new window]  and
YUE-FENG SHE Open the ORCID record for YUE-FENG SHE [Opens in a new window]
HAI-LIANG WU*
Affiliation:
School of Science, Nanjing University of Posts and Telecommunications, Nanjing210023, PR China
YUE-FENG SHE
Affiliation:
Department of Mathematics, Nanjing University, Nanjing210093, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

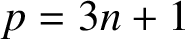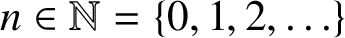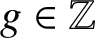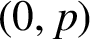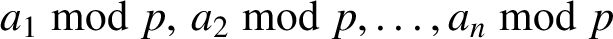Let $p=3n+1$ be a prime with $n\in \mathbb {N}=\{0,1,2,\ldots \}$ and let $g\in \mathbb {Z}$ be a primitive root modulo p. Let $0<a_1<\cdots <a_n<p$ be all the cubic residues modulo p in the interval $(0,p)$ . Then clearly the sequence $a_1 \bmod p,\, a_2 \bmod p,\ldots , a_n \bmod p$ is a permutation of the sequence 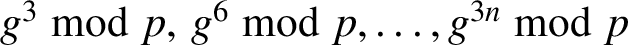$g^3 \bmod p,\,g^6 \bmod p,\ldots , g^{3n} \bmod p$ . We determine the sign of this permutation.

Keywords

permutationsprimitive rootscubes in finite fields

MSC classification

Primary: 11A15: Power residues, reciprocity
Secondary: 05A05: Permutations, words, matrices 11R18: Cyclotomic extensions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 2 , April 2022 , pp. 188 - 196
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by the National Natural Science Foundation of China (Grant No. 11971222).

The first author was also supported by NUPTSF (Grant No. NY220159).

References

Berndt, B. C., Evans, R. J. and Williams, K. S., Gauss and Jacobi Sums (Wiley, New York, 1998).Google Scholar
Borevich, Z. I. and Shafarevich, I. R., Number Theory (Academic Press, New York, 1966).Google Scholar
Brunyate, A. and Clark, P. L., ‘Extending the Zolotarev–Frobenius approach to quadratic reciprocity’, Ramanujan J. 37 (2015), 25–50.10.1007/s11139-014-9635-yCrossRefGoogle Scholar
Cox, D. A., Primes of the Form ${x}^2+n{y}^2$ : Fermat, Class Field Theory and Complex Multiplication (Wiley, New York, 1989).Google Scholar
Ireland, K. and Rosen, M., A Classical Introduction to Modern Number Theory, 2nd edn, Graduate Texts in Mathematics, 84 (Springer, New York, 1990).10.1007/978-1-4757-2103-4CrossRefGoogle Scholar
Lerch, M., ‘Sur un théorème de Zolotarev’, Bull. Internat. Acad. François Joseph 3 (1896), 34–37.Google Scholar
Petrov, F. and Sun, Z.-W., ‘Proof of some conjectures involving quadratic residues’, Electron. Res. Arch. 28 (2020), 589–597.10.3934/era.2020031CrossRefGoogle Scholar
Sun, Z.-W., ‘Quadratic residues and related permutations and identities’, Finite Fields Appl. 59 (2019), 246–283.10.1016/j.ffa.2019.06.004CrossRefGoogle Scholar
Sun, Z.-W., ‘On quadratic residues and quartic residues modulo primes’, Int. J. Number Theory 16(8) (2020), 1833–1858.10.1142/S1793042120500955CrossRefGoogle Scholar
Wang, L.-Y. and Wu, H.-L., ‘Applications of Lerch’s theorem to permutations of quadratic residues’, Bull. Aust. Math. Soc. 100 (2019), 362–371.10.1017/S000497271900073XCrossRefGoogle Scholar
Wu, H.-L. and She, Y.-F., ‘Jacobsthal sums and permutations of biquadratic residues’, Finite Fields Appl. 70 (2021), Article no. 101789.10.1016/j.ffa.2020.101789CrossRefGoogle Scholar
Zolotarev, G., ‘Nouvelle démonstration de la loi de réciprocité de Legendre,’ Nouv. Ann. Math. 11 (1872), 354–362.Google Scholar