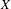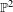3 results
Families of rational curves on holomorphic symplectic varieties and applications to 0-cycles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 18 December 2023, pp. 288-316
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
LAGRANGIAN FIBRATIONS OF HYPERKÄHLER FOURFOLDS
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 20 July 2020, pp. 921-932
- Print publication:
- May 2022
-
- Article
- Export citation
On the non-divisorial base locus of big and nef line bundles on K3[2]-type varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 52-78
- Print publication:
- February 2021
-
- Article
- Export citation

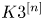
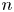
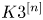
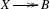 of a projective, irreducible symplectic fourfold
of a projective, irreducible symplectic fourfold