We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let G be a compact group, let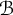 
$\mathcal {B}$ be a unital C
$^*$-algebra, and let 
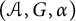$(\mathcal {A},G,\alpha )$ be a free C
$^*$-dynamical system, in the sense of Ellwood, with fixed point algebra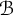 
$\mathcal {B}$. We prove that 
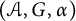$(\mathcal {A},G,\alpha )$ can be realized as the G-continuous part of the invariants of an equivariant coaction of G on a corner of 
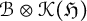$\mathcal {B} \otimes {\mathcal {K}}({\mathfrak {H}})$ for a certain Hilbert space 
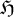${\mathfrak {H}}$ that arises from the freeness of the action. This extends a result by Wassermann for free and ergodic C
$^*$-dynamical systems. As an application, we show that any faithful 
$^*$-representation of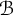 
$\mathcal {B}$ on a Hilbert space 
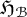${\mathfrak {H}}_{\mathcal {B}}$ gives rise to a faithful covariant representation of 
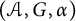$(\mathcal {A},G,\alpha )$ on some truncation of 
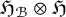${\mathfrak {H}}_{\mathcal {B}} \otimes {\mathfrak {H}}$.
